Definitions
250 likes | 288 Views
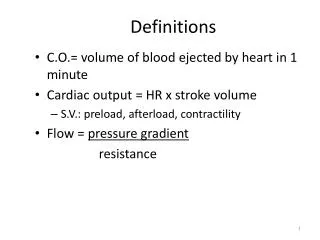
Definitions. Optimal alignment - one that exhibits the most correspondences. It is the alignment with the highest score . May or may not be biologically meaningful.

Definitions
E N D
Presentation Transcript
Definitions Optimal alignment - one that exhibits the most correspondences. It is the alignment with the highest score. May or may not be biologically meaningful. Global alignment - Needleman-Wunsch (1970) maximizes the number of matches between the sequences along the entire length of the sequences. Local alignment - Smith-Waterman (1981) gives the highest scoring local match between two sequences.
Pairwise Global Alignment • Global alignment - Needleman-Wunsch (1970) • maximizes the number of matches between the sequences along the entire length of the sequences. • Reason for making a global alignment: • checking minor difference between two sequences • Analyzing polymorphisms (ex. SNPs) between closely related sequences • …
Pairwise Global Alignment • Computationally: • Given: a pair of sequences (strings of characters) • Output: an alignment that maximizes the similarity
How can we find an optimal alignment? • ACGTCTGATACGCCGTATAGTCTATCTCTGAT---TCG-CATCGTC--T-ATCT • How many possible alignments? C(27,7) gap positions = ~888,000 possibilities • Dynamic programming: The Needleman & Wunsch algorithm 27 1
= (2n)!/(n!)2 = (22n /n ) = (2n) 2n n Time Complexity Consider two sequences: AAGT AGTC How many possible alignments the 2 sequences have?
Scoring a sequence alignment • Match/mismatch score: +1/+0 • Open/extension penalty: –2/–1ACGTCTGATACGCCGTATAGTCTATCT ||||| ||| || ||||||||----CTGATTCGC---ATCGTCTATCT • Matches: 18 × (+1) • Mismatches: 2 × 0 • Open: 2 × (–2) • Extension: 5 × (–1) Score = +9
Pairwise Global Alignment • Computationally: • Given: a pair of sequences (strings of characters) • Output: an alignment that maximizes the similarity
Needleman & Wunsch • Place each sequence along one axis • Place score 0 at the up-left corner • Fill in 1st row & column with gap penalty multiples • Fill in the matrix with max value of 3 possible moves: • Vertical move: Score + gap penalty • Horizontal move: Score + gap penalty • Diagonal move: Score + match/mismatch score • The optimal alignment score is in the lower-right corner • To reconstruct the optimal alignment, trace back where the max at each step came from, stop when hit the origin.
empty A A A C empty 0 -2 -4 -6 -8 A -2 1 -1 -3 -5 G -4 -1 0 -2 -4 C -3 -2 -1 -1 -6 Example • Let gap = -2 match = 1 mismatch = -1. AAAC A-GC AAAC -AGC
Time Complexity Analysis • Initialize matrix values: O(n), O(m) • Filling in rest of matrix: O(nm) • Traceback: O(n+m) • If strings are same length, total time O(n2)
Local Alignment • Problem first formulated: • Smith and Waterman (1981) • Problem: • Find an optimal alignment between a substring of s and a substring of t • Algorithm: • is a variant of the basic algorithm for global alignment
Motivation • Searching for unknown domains or motifs within proteins from different families • Proteins encoded from Homeobox genes (only conserved in 1 region called Homeo domain – 60 amino acids long) • Identifying active sites of enzymes • Comparing long stretches of anonymous DNA • Querying databases where query word much smaller than sequences in database • Analyzing repeated elements within a single sequence
GATCACCT GAT_ACCC empty G A T C A C C T 0 0 0 0 0 0 0 0 empty 0 0 0 0 0 G 0 0 0 0 0 A 0 0 0 0 1 T 0 0 0 0 0 A 0 0 C 0 0 0 0 C 0 0 0 C Local Alignment GATCACCT GATACCC • Let gap = -2 match = 1 mismatch = -1. 0 1 0 0 0 0 2 0 0 1 0 3 1 0 1 1 2 2 0 0 2 1 3 1 0 1 1 2 4 2 1 0 2 3 3
Smith & Waterman • Place each sequence along one axis • Place score 0 at the up-left corner • Fill in 1st row & column with 0s • Fill in the matrix with max value of 4 possible values: • 0 • Vertical move: Score + gap penalty • Horizontal move: Score + gap penalty • Diagonal move: Score + match/mismatch score • The optimal alignment score is the max in the matrix • To reconstruct the optimal alignment, trace back where the MAX at each step came from, stop when a zero is hit
exercise • Let: gap = -2 match = 1 mismatch = -1. • Find the best local alignment: CGATGAAATGGA
Semi-global Alignment Example: CAGCA-CTTGGATTCTCGG –––CAGCGTGG–––––––– CAGCACTTGGATTCTCGG CAGC––––G––T––––GG We like the first alignment much better. In semiglobal comparison, we score the alignments ignoring some of the end spaces.
Global Alignment Example: AAACCC A CCC • Prefer to see: • AAACCC • ACCC Do not want to penalize the end spaces
SemiGlobal Alignment Example: s = AAACCC t = ACCC
SemiGlobal Alignment Example: s = AAACCCG t = ACCC G 0 -1 -2 -1 2
SemiGlobal Alignment • Summary of end space charging procedures:
Pairwise Sequence Comparison over Internet Bioinformatics for Dummies
Significance of Sequence Alignment • Consider randomly generated sequences. What distribution do you think the best local alignment score of two sequences of sample length should follow? • Uniform distribution • Normal distribution • Binomial distribution (n Bernoulli trails) • Poisson distribution (n, np=) • others
Extreme Value Distribution • Yev = exp(- x - e-x )
“Twilight Zone” Some proteins with less than 15% similarity have exactly the same 3-D structure while some proteins with 20% similarity have different structures. Homology/non-homology is never granted in the twilight zone.