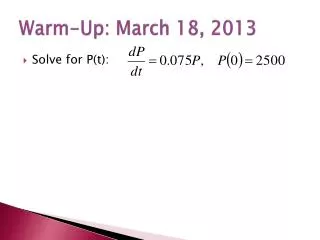1 / 9

Understanding Population Growth Models: Exponential vs. Logistic

Explore the dynamics of exponential and logistic population growth models, differential equations, and carrying capacity. Solve homework questions with examples and exercises from Sections 6.5 and 6.6 in this comprehensive study guide.

lowri
Download Presentation

Understanding Population Growth Models: Exponential vs. Logistic

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Warm-Up: March 18, 2013 • Solve for P(t):

  2. Homework Questions?

  3. Population Growth Section 6.5

  4. Exponential Population Growth Model • Many populations grow at a rate proportional to the size of the population. • where k is the relative growth rate. • The resulting exponential growth model is • We usually use t=0 as the first year of our model

  5. Example 1 • Springfield has a current population of 36000 and is growing at a relative rate of 2.3%. • Write a differential equation for the population. • Find a formula for the population P(t). • Superimpose the graph of the population function on a slope field for the differential equation.

  6. Logistic Population Growth Model • Populations cannot increase forever. • Environmental factors often limit the population to some maximum value, M, called the carrying capacity. • The logistic growth model is found from the following logistic differential equation:

  7. Example 2 • Find k and the carrying capacity for the population represented by

  8. Logistic Growth Model • The solution to • Is given by • Where A is a constant found using the given initial condition

  9. Assignment • Read Section 6.5 (pages 342-346) • Page 347 Exercises #1-15 odd • Read Section 6.6 (pages 350-355)

More Related