Understanding Spurious Regression Through Simulated Data Generation Processes

Jan 16, 2026

140 likes | 301 Views

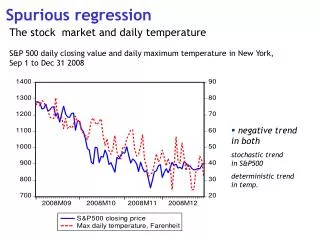
This example illustrates a data generation process demonstrating spurious regression. By generating two time series, Y and X, using autoregressive relationships and random noise, we reveal how these series can appear correlated despite lacking a causal link. The procedure involves iterating through time points, applying defined parameters (alpha, beta), and outputting results for analysis. Knowing this phenomenon is vital for correctly interpreting statistical relationships in time series data.

ross-burris

Download Presentation

Understanding Spurious Regression Through Simulated Data Generation Processes

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

Spurious Regression-An Example
Data Generation Process • new; • format /m1 /rd 9,3; • apha=3; beta=1; • T=100; • Y=zeros(T,1); • X=zeros(T,1); • e1=Rndn(T,1); • e2=Rndn(T,1); • @ Data Generation Process @ • Y[1,1]=0; X[1,1]=0; • i=2; • do until i>T; • Y[i,1]=apha+beta*Y[i-1,1]+4*e1[i,1]; • X[i,1]=apha+beta*X[i-1,1]+2*e2[i,1];
i=i+1; • endo; • Output file=d:\Enclass\Spus\level.out reset; • Y~X; • Output off; • Output file=d:\Enclass\Spus\Diff.out reset; • (Y[2:100,1]-Y[1:99,1])~(X[2:100,1]-X[1:99,1]); • Output off;