1 / 27

Quadrature

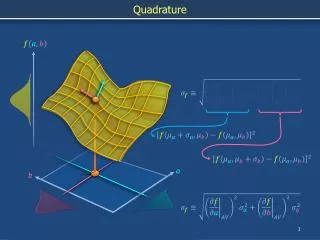
Quadrature. 二阶 : 中点公式 :. 梯形公式 :. 四阶公式 :. Simpson’s 1/3 rd Rule. Boole ’ s rule,The 6-th Newton-Cotes rule (the first step of Romberg integration) The extrapolated Simpson ’ s rule. #include <stdio.h> #include <stdlib.h> #include <math.h> #define TRUE 1

montgomery-arjun
Download Presentation

Quadrature

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Quadrature

  2. 二阶: 中点公式: 梯形公式: 四阶公式: Simpson’s 1/3rd Rule

  3. Boole’s rule,The 6-th Newton-Cotes rule (the first step of Romberg integration) The extrapolated Simpson’s rule.

  4. #include <stdio.h> #include <stdlib.h> #include <math.h> #define TRUE 1 struct t_bc{float a, b, h;} bc; void main() { int isimp, k, n; float s; void simps(), trapz(); printf( "\nComputer Soft/C7-1 Trapezoidal/Simpson's Rule \n\n" ); while( TRUE ){ printf( "Type 0 for trapezoidal, or 1 for Simpson's\n " ); scanf( "%d", &isimp ); printf( "Number of intervals ? " ); scanf( "%d", &n ); printf( "Lower limit of integration? " ); scanf( "%f", &bc.a ); printf( "Upper limit of integration? " ); scanf( "%f", &bc.b ); bc.h = (bc.b - bc.a)/n; if( isimp == 0 ){ trapz( &s, n ); /*-- Trapezoidal rule */ } else{ simps( &s, n ); /*-- Simpson's rule */ } printf( "-----------------------------------------\n" ); printf( " Result = %g \n", s ); printf( "-----------------------------------------\n" ); printf( "\nType 1 to continue, or 0 to stop.\n"); scanf( "%d", &k ); if( k != 1 ) exit(0); } }

  5. void simps(ss, n) /* Simpson's rule*/ float *ss; int n; { int i, ls; float sum, s, w, x; double func(); s = 0; sum = 0; if( n/2*2 == n ) ls = 0; else { ls = 3; for( i = 0; i <= 3; i++ ) { /* Simpson's 3/8 rule if n is odd */ x = bc.a + bc.h*i; w = 3; if( i == 0 || i == 3 ) w = 1; sum = sum + w*func( x ); } sum = sum*bc.h*3/8L; if( n == 3 ) return; } for( i = 0; i <= (n - ls); i++ ){ /* Simpson's 1/3 rule */ x = bc.a + bc.h*(i + ls); w = 2; if( (int)( i/2 )*2 + 1 == i ) w = 4; if( i == 0 || i == n - ls ) w = 1; s = s + w*func( x ); } *ss = sum + s*bc.h/3; return; } void trapz(ss, n) /* Trapezoidal rule */ float *ss; int n; { int i; float sum, w, x; double func(); sum = 0; for( i = 0; i <= n; i++ ){ x = bc.a + i*bc.h; w = 2; if( i == 0 || i == n ) w = 1; sum = sum + w*func( x ); } *ss = sum*bc.h/2; return; } double func(x) float x; { float func_v; func_v = pow(1 + pow(x/2, 2), 2)*3.14159; return( func_v ); }

  6. Composite Simpson numerical integration a = 0;b = 1; M = 10; H = (b-a)/M; % 2M intervals x = linspace(a,b,M+1); fpm = feval('fquad',x); fpm(2:end-1) = 2*fpm(2:end-1); csq = H*sum(fpm)/6; x = linspace(a+H/2,b-H/2,M); fpm = feval('fquad',x); csq = csq + 4/6*H*sum(fpm);

  7. quad 基于变步长Simpson公式 (recursive adaptive Simpson quadrature) quad8 基于Newton-Cotes公式 (adaptive recursive Newton-Cotes 8 panel rule) quadl adaptive Lobatto quadrature % 1 f = inline('sin(x)/x'); f = vectorize(f); Q = quad(f,realmin,pi) % 2 anonymous function, beginning with MATLAB 7 f = @(x) sin(x)/x Q = quad(f,realmin,pi) % 3 use an M-file Q = quad(@sinc,0,pi)

  8. Dblquad 二重积分 Triplequad 三重积分 计算 %1 function f = fxy(x,y) f = exp(-x.^2/2).*sin(x.^2+y.^2); I = dblquad('fxy',-2,2,-1,1) %2 I = dblquad(inline('exp(-x.^2/2).*sin(x.^2+y.^2)','x','y'),-2,2,-1,1) 符号计算 int

  9. % integrating discrete data x = 0:10; y = x; % composite trapezoid rule T = sum(diff(x).*(y(1:end-1)+y(2:end))/2)

  10. Gauss-Legendre公式 Gauss-Chebyshev公式 Gauss-Laguerre公式 Gauss-Hermite公式 n点求积公式若具有2n-1阶代数精度就成为 Gauss 型求积公式.

  11. 定理： 其中 是正交多项式的实根， 是权函数，

  12. 三项递推：

  13. 勒让德多项式(Legendre) [-1,1] , (x)=1 递推关系: P0(x)=1, P1(x)=x,

  14. Legendre多项式

  15. Christoffel-Darboux identity 设 则 对Legendre多项式

  16. 切比雪夫多项式(Chebyshev) Tn(x)=cos(narccosx) 递推关系: T0(x)=1 , T1(x)=x , T2(x)=2x2-1 , T3(x)= 4x3-3x,………

  17. 埃尔米特多项式 (Hermite) • (- ,+), (x)=e-x2 Hermite多项式的三项递推关系

  18. 拉盖尔多项式(Laguerre) [0,+), (x)=e-x Laguerre多项式的三项递推关系

  19. 无穷积分 令 Gauss-Laguerre方法(定义在[0,∞),无复合公式)

  20. 补充: 分段多项式插值 三阶Hermite插值 区间 [xi, xi+1], s=x-xi, h=hi= xi+1-xi

  21. 区间 [xi, xi+1]

  22. 三次样条插值

  23. 区间 [xi, xi+1], s=x-xi, yi=f(xi), di=f’(xi) 区间 [xi-1, xi],

  24. 端点条件: • 固定斜率 • 自然端点 • 非节点 代入d3

  25. The road to wisdom? Well, it’s plain and simple to express: Err and err and err again but less and less and less PIET HEIN, Grooks(1966)

More Related