M arkow- K etten
240 likes | 406 Views
M arkow- K etten. Jens Keienburg, Nora Rieber, Samuel Bandara, Felix Bonowski . Übersicht. Definitionen Veranschaulichung; ‚Bienen-Modell‘ die Übergangsmatrix die Grenzmatrix Anwendung in Genomics. Stochastischer Prozess. Folge von Zufallsexperimenten

M arkow- K etten
E N D
Presentation Transcript
Markow-Ketten Jens Keienburg, Nora Rieber,Samuel Bandara, Felix Bonowski
Übersicht • Definitionen • Veranschaulichung; ‚Bienen-Modell‘ • die Übergangsmatrix • die Grenzmatrix • Anwendung in Genomics
Stochastischer Prozess • Folge von Zufallsexperimenten • beschreibbar durch Funktion X(t), t g T • X(t): ‚Zufallsvariable‘ • T: ‚Parameterraum‘ • M: ‚Zustandsraum‘; M = {X(t) | t g T} • Bsp: n-maliger Münzwurf
Markow-Ketten • diskret in Zeit und Raum • Besonderheit: Wahrscheinlichkeit eines Zustands hängt nur von der Wahrscheinlichkeit des vorherigen ab • Markow-Kette ist bestimmt durch • Anfangsverteilung • Übergangswahrscheinlichkeiten • ihren Zustandsraum
Chrysantheme Akelei Tulpe Geranie Das Bienen-Modell • Wohin geht die Biene als nächstes?
Chrysantheme 1/2 1/3 Akelei Tulpe 1/3 1/2 1/3 1/4 1/3 1/3 1/4 A G C T 1/3 A 1/3 1/3 1/3 0 1/4 G 1/4 1/4 1/4 1/4 Geranie C 1/2 0 0 1/2 1/4 T 0 1/3 1/3 1/3 Übergangswahrscheinlicheiten
Die Übergangsmatrix • P = • Allgemein:in der i-ten Zeile und der k-ten Spalte Wahrscheinlichkeit pik für einen Übergang vom Zustand i in den Zustand k
Die Übergangsmatrix • P = • Matrix ist stochastischpikg [0;1] i,k = 1,2,...,N
Chrysantheme Akelei Tulpe Geranie Mehrstufige Übergänge • Wo ist die Biene in n Zügen? • Grenzwert?
Definitionen • p(n)= (p1(n), p2(n), …, PN(n)) Wahrscheinlichkeiten für jeden Zustand nach n Durchgängen • Anfangsverteilung: p(0) • z.B. (1 0 0 0) Biene sitzt auf Akelei • oder (0.25 0.25 0.25 0.25) Anfangsort unbekannt
Spätere Verteilungen • Zustände auf mehreren Wegen erreichbar • Nächster Zustand durch Anwendung der Übergangsmatrix zugänglich • p(n+1)= P*p(n) n Beispiel: = p(n) p(0) *
Langfristiges Verhalten • Die Matrix limn®¥(P)n heißt Grenzmatrix • Wenn sie existiert erlaubt sie Aussagen über das langfristige Verhalten des Systems. • In unserem Beispiel: • limn®¥(P)n =
Diskussion des Beispiels • In unserer Grenzmatrix sind die Elemente einer Spalte gleich (Ergodische Matrix) • Jede Anfangsverteilung führt im Grenzwert zur gleichen Verteilung p(¥)= (0,265 0,235 0,235 0,264) • Das dann der Fall, wenn es zwischen allen Zuständen irgendeinen zulässigen Weg gibt.
Chrysantheme Akelei Tulpe Geranie Wahrscheinlichkeiten von Pfaden • Pfad: (C T G C A) p(CTGCA)=p(C®T)*p(T®G)…*P(G®A)
C C A A T T G G Zwei Gärten… Garten 1 mit Übergangsmatrix P1 Gegeben: Die Biene hat die Blumen in der Reihenfolge CTGATC besucht. Frage: In welchen Garten war sie? Garten 2 mit Übergangsmatrix P2
Genomics Problematik : Entschlüsselung des Genoms Welche Bereiche codieren ? Wo befinden sich Gene?
Genomics Gene Prediction : Codierende und nicht codierende DNA-Sequenzen besitzen unterschiedliche Übergangswahrscheinlichkeiten. Mit Hilfe von Markovketten lassen sich Gene zuverlässig finden !
Genomics Definition : Ein Open Reading Frame (ORF) ist eine Gensequenz, die von einem Start- und einem Stopcodon terminiert wird. Ein Gen ist ein codierender ORF Jeder ORF ist ein möglicher Kandidat für ein Gen. Wesentlich mehr ORF als Gene.
Genomics Markowmodell : Xt(b) sei Zufallsvariable T ist Indexmenge mit T ={1, ...N}, wobei N = Anzahl der Basen Zustandsraum B ={A, C, T, G}, und b1, b2, ... g B Markow‘sche Eigenschaft : P( Xn(b) = b1 | Xn-1(b) = b1 , Xn-2(b) = b2, ... ) = P( Xn(b1) | Xn-1(b2) )
Genomics Produkt aller Wahrscheinlichkeiten ist ein Maß für die Wahrscheinlichkeit eines Gens. Genom : Abhängigkeit Xn von Xn-1, ... Xn-j mit 0 < j < 8 ist Grad der Markowkette Auf jedes j-Tupel von Basen folgt eine Base. Erfassung der Übergangswahrscheinlichkeiten mit einer höher dimensionalen Übergangsmatrix.
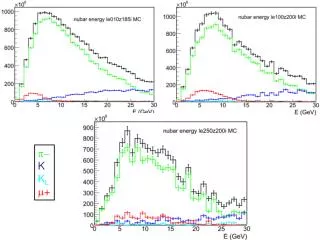
Genomics Versuch am Genom von E. Coli liefert folgende Ergebnisse
Gene Prediction Ergebnisse : 1) Der Algorithmus identifiziert ein Gen mit einer Wahrscheinlichkeit von 94% richtig. 2) ORFs werden zu weniger als 10% fälsch- licherweise als Gene erkannt.