1 / 18

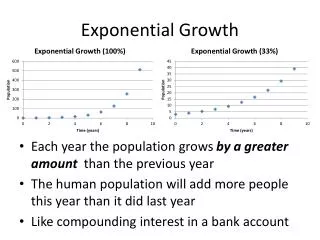
Exponential Growth

Exponential Growth. Exponential Growth y = a (1 +b) t y = final amount after a period of time a= original amount t = time b = percent of increase (as a decimal) (1 + b ) is called the multiplier If multiplier is greater than 1, it is a growth problem.

sook
Download Presentation

Exponential Growth

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Exponential Growth

  2. Exponential Growthy = a (1 +b)t y = final amount after a period of timea= original amountt = timeb = percent of increase (as a decimal)(1 + b ) is called the multiplierIf multiplier is greater than 1, it is a growth problem

  3. Finding the multiplierex. Growth of 5%Change 5% to a decimal (.05)1+ .05 = 1.051.05 is the multiplier

  4. Ex. Growth of 45%45% = .451 + .45 = 1.451.45 is the multiplier

  5. Ex. Growth of 0.8%0.8% = .0081 + .008 = 1.0081.008 is the multiplier

  6. Ex. A certain quantity DoublesIf sometime doubles, it is increasing by 100%100% = 1.01+ 1.0 = 2 Therefore, 2 is the multiplier

  7. A quantity triplesIf something triples it is increasing by 200% 200% = 2.01 + 2.0 = 33 is the multiplier

  8. Finding percent of growthPercent of growth= amount of changeoriginal amountMake this decimal a %This is the % of change

  9. Ex. A quantity changes from 20 to 35. Find the percent of increase.Amount of change = 15 Orignal Amount = 20 = .75 = 75%75% is the percent of increase

  10. Ex. A price increases from $40 to $45. Find the % of increase 5 = 1 40 8= .125 = 12.5%

  11. Ex. The population of a town increases from 60,000 to 120,000. Find the % of increase.60,00060,000= 1.0 = 100%100% is the percent of increase

  12. Examples of Exponential Growth

  13. Ex. The price of a gallon of milk increases at a rate of 2% per year. In 1990, a gallon of milk cost $2. How much would the gallon of milk be expected to cost in 2002?Final cost=original amt (1 +% ofincrease)time cost in 2002 = 2(1+.02)12 = 2(1.02)12 = $2.54

  14. Ex. The population of a town is increasing at a rate of 6% every 2 years. The population was 12,000 in 1980. What would the population be expected to be in 2000?Population in 2000 = 12,000(1 + .06)10 = 12,000(1.06)10 21,490

  15. The # of deer in a particular forest is estimated to be about 352 right now. The population has been growing at a rate of 12% What was the approximate population 5 years ago?

  16. 352 = a (1.12)5 352 = a(1.12)5 (1.12)5 = (1.12)5200 ≈ a

  17. The value of an investment has grown at a rate of 2% per year It was originally valued at $20,000. It is now valued at $22,974. How much time has gone by?

  18. 22,974 = 20,000(1.02)t 22,974 = 20,000(1.02)t 20,000 = 20,0001.15 ≈ (1.02)t *Next use “guess and check” for values of “t”(1.02)5 ≈ 1.10(1.02)6 ≈ 1.13(1.02)7 ≈ 1.15This last one is closest to 1.15 so 7 years have gone by.

More Related