Lecture 8
130 likes | 370 Views
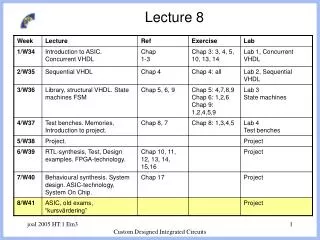
Lecture 8. Magnetic Dipoles. Comparing with equation (1). Surface Field from a dipole. -m. -. +m. +. M is magnetic moment; M=m Δz=JV. Magnetic Susceptibility. H. I. Z. Magnetic north. x. z. R. function F=magdike(x,x0,k,Fe,w,z1,I,beta);

Lecture 8
E N D
Presentation Transcript
Lecture 8 Magnetic Dipoles
Surface Field from a dipole -m - +m + M is magnetic moment; M=m Δz=JV
H I Z Magnetic north x z R
function F=magdike(x,x0,k,Fe,w,z1,I,beta); %%%% magnetic field from a vertical dike using Telford Eq.3.44c %%%% I = inclination (degrees) %%%% beta = strike (degrees) of dike anticlockwise from North magnetic %%% x = coordinates %%% x0 = the dike location %%% k = susceptibility factor %%% Fe = Earth's field %%% w = dike width %%% z1 = depth to top of dike %%% I = inclination in degrees %%% Bring angles to radians I=I*pi/180;beta=beta*pi/180; %%% Constant term A=2*Fe*k; xd1=x-x0; xd2=x-x0-w; phi1=atan2(z1,xd1); r1=sqrt(z1^2+xd1.^2); phi3=atan2(z1,xd2); r3=sqrt(z1^2+xd2.^2); term1=sin(2*I)*sin(beta)*log(r3./r1); term2=(cos(I)^2*sin(beta)^2-sin(I)^2)*(phi1-phi3); F=A*(term1+term2); % plot(x,F,'r') % figure(1)
MAGNETIC FIELD FROM A DIKE ϕ2 0 X X0 Φ1 r1 r2 D
%%%%%% plots mag data for day 2 Trona Field trip. %%%%% clf data=load('magnetic_readings_20120128.dat'); n1=47;n2=145; y=data(n1:n2,3)'; lat=data(n1:n2,6); lon=data(n1:n2,7); y=y-mean(y); [X,Y]=deg2utm(lat,lon); x=X-420000; plot(x,y,'*') Fe=50000; %%% Dike 1 I=60; beta=10; x0=a(2); k=a(1); z1=a(3);w=20; F1=magIdike(x,x0,k,Fe,w,z1,I,beta); f=F1-mean(F1); f=f'; plot(x,y,'*',x,f,'linewidth',2)