Equation différentielle
320 likes | 615 Views
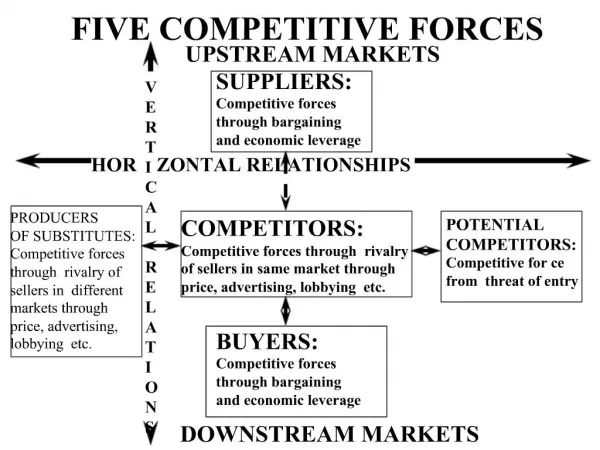
Equation différentielle. Elaboré par M. NUTH Sothan. I. Définition. Déf .: F(x, y, y’) = 0 (1) où x est une variable, y est une fonction de variable x et y’ sa dérivée, s’appelle équation différentielle du 1 er ordre .

Equation différentielle
E N D
Presentation Transcript
Equation différentielle Elaboré par M. NUTH Sothan
ED1 I. Définition Déf.: F(x, y, y’) = 0 (1) où x est une variable, y est une fonction de variable x et y’ sa dérivée, s’appelle équation différentielle du 1er ordre. On peut résoudre par rapport y’ : y’=f(x, y) (2)
ED1 I. Définition… On peut écrire aussi sous forme : Ex.:
ED1 II. Solution Considérons : y’=f(x, y) (1) Déf.1: La solution de (1) est une fonction y = (x), x (a, b) qui vérifie (1). Ex.: y=x3est une solution de
ED1 II. Solution… Déf.2: La solution générale de (1) est une fonction y=(x, c), xG et c est une constant, qui vérifie (1) et pour toute condition initiale (x0 , y0) G, il existe uniquement c=c0 tel que la fonction y=(x, c0) implique (x0 , c0)=y0 ,
ED1 II. Solution… Déf.3: La solution partielle de (1) est une fonction y=(x, c0), xG et c0 est une constant, qu’on obtient de solution générale en donnant la condition initiale Ex.: y’= 3x2 La solution générale est y=x3 + c Avec la CI y(0)=1 c = 1. La solution partielle est y=x3 + 1.
ED1 III. ED du 1er ordre à variable séparées 1. L’équation sous forme y’=f1 (x) f2 (y) (1) où f1 (x) et f2 (y) sont continues est dites Equation Différentielle du 1er ordre à variables séparées. Du (1), on a : (2) (3)
ED1 III. ED du 1er ordre à variables séparées… 2. L’équation sous forme y’=f (ax+by+c), ( b 0) (4) En posant u=ax+by+c , (4) devient (1). Ex.:
ED1 IV. ED du 1er ordre hormogène 1. L’équation sous forme (1) (2) Ex.1:
ED1 IV. ED du 1er ordre hormogène… 2. L’équation sous forme (3) où
ED1 IV. ED du 1er ordre hormogène… En posant x=u+, y=v+ , et en résoudre le système on obtient l’EDH de variable u et v . Si =0, on pose u=ax+by , on obtient l’ED à variable séparée.
ED1 IV. ED du 1er ordre hormogène… Ex.2: a/ b/ c/
ED1 V. ED Linéaire du 1er ordre L’équation sous forme (1) est dite EDL du 1er ordre. Si f(x)=0 alors, (1) est hormogène, et sinon est non hormogène.
ED1 V. ED Linéaire du 1er ordre… Méthode 1: Considérons (2) Trouvons la solution Générale Hormogène :
ED1 V. ED Linéaire du 1er ordre… Trouvons la Solution Particulière Non Hormogène : Posons SPNH. En remplaçant dans (1), on trouve C(x) et en on trouve la Solution Générale de (1). Méthode 2: La Solution Générale de (1) est proposée sous forme y=u(x)v(x).
ED1 V. ED Linéaire du 1er ordre… En remplaçant y=u(x)v(x), on obtient :
ED1 V. ED Linéaire du 1er ordre… Ex.: a) b) c)
ED1 VI. ED sous forme différentielle totale L’équation sous forme : (1) est dite ED sous forme différentielle totale si (2) Alors, il existe u(x, y) telle que (3)
ED1 VI. ED sous forme différentielle totale… En comparant (1) et (3), on a : Pour résoudre (1), on fait l’intégrale Or
ED1 VI. ED sous forme différentielle totale… Ex.1: a/ b/ c/ d/
ED1 VI. ED sous forme différentielle totale… En cas on peut trouver (x) ou (y) qui s’appelle facteur intégrant qui vérifie Ex.2: a/ b/ c/
ED1 VII. Autre type de l’ED de 1er ordre 1. Equation de Bernoulli : (1) En divisant (1) par yn, on obtient (2) En posant z=y1-n, on obtient (3)
ED1 VII. Autre type de l’ED de 1er ordre… Ex.1: a/ b/ c/
ED1 VII. Autre type de l’ED de 1er ordre… 2. Equation sous forme F(x, y, y’)=0 (4) Si (4) est une équation de second degré par rapport y’, et si on obtient deux racines : y’=f1(x, y) et y’=f2(x, y). (5) Alors, la SG est sous forme : (x,y,C) = 1(x,y,C) 2(x,y,C) = 0 (6) En plus, il existe la solution singulière de (x,y,C) = 0 et ’C(x,y,C) = 0 (7)
ED1 VII. Autre type de l’ED de 1er ordre… Ou le résultat d’élimination y’=p de F (x,y,p) = 0 et F’p(x,y,p) = 0 (8) Ex.2: xy’ 2+2xy’ – y = 0 Posons: y’=p. On obtient xp2+2xp – y = 0
ED1 VII. Autre type de l’ED de 1er ordre… 3. Equation sous forme x = (y, y’) La SG est sous forme paramètre de système : Analogiquement, pour y = (x, y’) : La SG est sous forme paramètre de système :
ED1 VII. Autre type de l’ED de 1er ordre… Ex.3: a/ b/ c/ d/
ED1 VII. Autre type de l’ED de 1er ordre… 4. Equation de Clairaut : (9) Pour résoudre on pose y’=p(x), on obtient deux cas de : (10) a) b)
ED1 VII. Autre type de l’ED de 1er ordre… 5. Equation de Lagrange : (11) On peut faire la même façon comme au dessus. Ex.4: a/ b/
ED1 VIII. Exemple 1. 2. 3. 4. 5. 6.
ED1 VIII. Exemple… 7. 8. 9. 10. 11. 12.