1 / 36

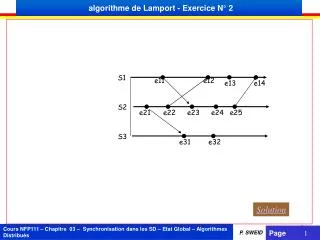
algorithme de Lamport - Exercice N° 2

algorithme de Lamport - Exercice N° 2. S1. e11. e12. e13. e14. S2. e21. e22. e23. e24. e25. S3. e31. e32. Solution. Remarques. P 1. P 2. P 3. Q 1. Q 2. H( E 1 ) < H( E 2 ) n'implique pas E 1 --> E 2. H( E 1 ) < H( E 2 ) ? E 1 --> E 2 Exemple :

noah-hendricks
Download Presentation

algorithme de Lamport - Exercice N° 2

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. algorithme de Lamport - Exercice N° 2 S1 e11 e12 e13 e14 S2 e21 e22 e23 e24 e25 S3 e31 e32 Solution

  2. Remarques P 1 P 2 P 3 Q 1 Q 2 • H( E 1 ) < H( E 2 ) n'implique pas E 1 --> E 2 • H( E 1 ) < H( E 2 ) ?E 1 -->E 2 • Exemple : • H( Q 1 ) < H( P 2 ) < H( P 3 ) • H( Q 1 ) < H( Q 2 ) • Mais P 3 Q 2 et Q 2 P 3 • La relation → définit un ordre partiel sur les événements d’un calcul réparti.

  3. Passé de l'événement Définitions Passé de l'événement A ensemble des événements B tel que B A • exemple :Passé ‘ historique ’ de l'événement e : • hist(e) = {ensemble des e' tels que e'  e} Passé hist(e33) = {e11 e21 e22 e23 e24 e25 e31 e32 e33}

  4. Passé de l'événement - exemple exemple :Passé ‘ historique ’ de l'événement e hist(e) = {ensemble des e' tels que e'  e} hist(e33) = {e11 e21 e22 e23 e24 e25 e31 e32 e33} Définition : (projection de hist(e) sur P i )

  5. Algorithme de L. Lamport : exemple complet e11 e12 e13 e14 e15 e16 e17 e18 e19 S1 1 2 3 e2 10 e24 e26 e21 e28 e29 S2 e22 e23 e25 1 e27 e32 e31 e33 e34 e35 e36 e37 e39 e3 10 e38 S3 1 La figure suivante donne la valeur des estampilles logiques scalaires associées en appliquant la méthode décrite précédemment à des événements de 3 sites entre lesquels des messages estampillés sont échangés. 4 6 7 11 12 13 9 2 3 5 16 8 4 6 10 14 4 5 6 7 8 9 13 14 15

  6. Ordre total des événements -1- • A un événement e on peut alors associer trois ensembles d'événements : Passé(e): ensemble des événements antérieurs à e dans l'ordre causal (e appartient à cet ensemble); Futur(e): ensemble des événements postérieurs à e dans l'ordre causal (e appartient à cet ensemble); Concurrent(e): ensemble des événements concurrents avec e.

  7. Ordre total des événements -2- • Considérons l'événement e27. Il appartient à son propre passé et est précédé directement par e26 et e35. • - On a Passé(e27) = {e27} + Passé(e26) + Passé(e35) - Passé(e25) = {e25} + Passé(e24)- Passé(e24) = {e24} + Passé(e23) + Passé(e11) - Passé(e23) = {e23} + Passé(e22)- Passé(e22) = {e22} + Passé(e21) + Passé(e31) - Passé(e21) = {e21} - Passé(e31) = {e31} - Passé(e11) = {e11} - Passé(e14) = {e14} + Passé(e13)- Passé(e13) = {e13} + Passé(e12)- Passé(e12) = {e12} + Passé(e11) + Passé(e21) - Passé(e35) = {e35} + Passé(e34) - Passé(e34) = {e34} + Passé(e33) + Passé(25) - Passé(e33) = {e33} + Passé(e32) - Passé(e32) = {e32} + Passé(e11) + Passé(e23)

  8. Ordre total des événements -3- Le calcul de Passé(e27) suppose donc le calcul de celui de e26 et e35. - On a Passé(e26) = {e26} + Passé(e25) + Passé(e14) Par conséquent Passé(e27) = {e11, e12, e13, e14, e21, e22, e23, e24, e25,e26 , e27, e31, e32,e33,e34,e35} Par un calcul analogue, on obtient: Futur(e27) = {e17, e18, e19, e27,e28, e29, e2 10, e2 11, e3 8, e3 9, e3 10} Finalement les événements n'appartenant ni à Passé(e27), ni à Futur(e27) sont concurrents avec e27. On a donc Concurrent(e27) = {e15, e16, e36, e37}

  9. Ordre total des événements -4- • Remarques : • Les 2 règles précédentes ne résolvent pas le problème des événements concurrents. • L'ordre n'est que partiel. • L’ordre des événements ainsi défini, n’est pas un ordre strict : • Plusieurs événements peuvent porter la même valeur. • C ’est le cas (sur notre exercice N°.2) des événements e15, e26 et e34 appartenant respectivement aux S1, S2 et S3 et qui ont chacun 6 comme valeur de date. { E  E ’ => H(E) < H(E ’) mais H(E) < H(E ’) non E  E ’ } • Il est facile de rendre cet ordre strict « total  » en modifiant légèrement le système de datation : • « la date d ’un événement sur un site est obtenue en adjoignant à la valeur de l ’horloge scalaire de ce site l’identification du site(par exemple un entier attribué artificiellement ou une adresse IP ou physique) ».

  10. Ordre total des événements -5- • Pour établir un ordre total des événements, il faut départager les événements concurrents : • L ’horloge logique ,Hi (Ei) d’un événement Eidu site Si est un couple (Hi , i) • On a Eiprécède EjEiEj, si et seulement si • ou bienHi(Ei) < Hj (E j ) • oubien Hi(Ei) =H j (Ej) eti < j [ Hi(Ei) , i]

  11. Ordre total des événements -6- • Sur notre exemple : • si on ordonne les sites par l'ordre de leurs numéros , S1 précède S2 qui précède S3 et donc du point de vue des événements, e15 précède e26 qui précède e34. • l'ordre ainsi défini respecte la causalité : • si un événement eprécède un événement e', • la valeur de son estampille logique est inférieure à celle de e'.

  12. Ordre total des événements -7- • l'ordre ainsi défini respecte la causalité : • si un événement e précède un événement e', la valeur de son estampille logique est inférieure à celle de e'. Si on considère les événements dans le passé de l'événement e27, ils ont tous une estampille scalaire inférieure à celle de e27(8.2). De manière duale, les événements du futur de e27ont une estampille supérieure à celle de 8.2. L'ordre ainsi défini est total : il induit une chaîne de tous les événements. Sur notre exemple, la chaîne induite par ce système de datation est : e11 e21 e31 e12 e22 e13 e23 e14 e24 e32 e25 e33 e15 e26 e34 e16 e35 e27 e36 e28 e37 e29 e17 e18 e19 e38 e2 10 e39 e3 10 e2 11

  13. Ordre total des événements -8- e11 e12 e13 e14 e15 e16 e17 e18 e19 S1 1 2 3 4 6 7 11 12 13 e2 10 2 3 e24 5 e26 16 e21 8 e28 e29 S2 4 6 10 1 e22 e23 e25 9 14 e27 e38 e32 e31 e33 e34 e35 e36 e37 e39 e3 10 S3 4 1 5 6 7 8 9 13 14 15 e11 e21 e31 e12 e22 e13 e23 e14 e24 e32 e25 e33 e15 e26 e34 e16 e35 e27e36 e28 e37 e29 e17 e18 e19 e38 e2 10 e39 e3 10 e2 11

  14. Ordre total des événements -9- • Tous les événements dans Passé(e27) apparaissent avant e27 dans cette chaîne. • Tous les événements dans Future (e27) apparaissent après e27 dans cette chaîne. • Des événements concurrents sont quant à eux artificiellement ordonnés. • Si nous considérons les événements incomparables e27 et e16 de notre exemple (nous avons vu que e16 appartient à concurrent(e27)), le système de datation fait que e16 apparaît antérieur à e27. Parmi les événements concurrents de e27, les événements e15 et e16apparaissent antérieurs alors que e36, e37 et e38apparaissent postérieurs. e11 e21 e31 e12 e22 e13 e23 e14 e24 e32 e25 e33 e15 e26 e34 e16 e35 e27e36 e28 e37 e29 e17 e18 e19 e38 e2 10 e39 e3 10 e2 11

  15. Exercice N° 1 - Algorithme de L. Lamport • 1- Initialiser toutes les Hi à zéro : H i = 0  i • 2 - A chaque événement local (Ei) sur un site Si • H i := Hi + 1 • Ei: est daté par H i • Conséquence : • E 1 et E 2 sont dans le processus P i et que E 1 --> E 2 alors • H i (E 1 ) < H i (E 2 ). • 3- Chaque message émis par Pi doit estampillée par la date de son émission : (m, TS(m)), avec TS(m) = H(Emission) = H i • 4- A la réception d ’un message (m, TS(m)) sur site Sj : • H j = max(TS(m) ,H j ) + 1= max(H i ,H j ) + 1

  16. Exercice N° 1 - Algorithme de L. Lamport 0 e11 Initialiser toutes les Hi à zéro : H i = 0  i e12 H i := Hi + 1 S1 m1 TS(m1) = 2 e22 0 S2 TS(m2) = 4 e21 m2 e31 0 S3 e32 H 2 (e21) = max(2 ,0 ) + 1 = 3 H 3 (e32) = max(4 ,1 ) + 1 = 5 1 2 3 4 H j = max(TS(m) ,H j ) + 1 = max(H i ,H j ) + 1 5 1 Retour

  17. Exercice N°2 - Algorithme de L. Lamport 1 0 S1 e11 e12 e13 e14 1 0 S2 e21 e22 e23 e24 e25 0 S3 e31 e32 3 4 6 2 3 4 5 2 3 Retour

  18. Exercice N°3 - Estampillage vectorielle 1 - Vi[1,…,N] = (0,…..,0) 2 - Vi[i] := Vi[i] + 1 e11 e12 S1 3 - Vi[i] := Vi[i] + 1 Vi[j] := max(Vi[j], EVm[j]) pour tous j = 1,…N, j  i e22 S2 (0,0,0) e21 S3 e31 e32 (0,0,0) (0,0,0) (2,0,0) (1,0,0) (2,2,0) (2,1,0) (0,0,1) (2,2,2) Retour

  19. Exercice N°3 - Estampillage vectorielle 1 - Vi[1,…,N] = (0,…..,0) 3 - Vi[i] := Vi[i] + 1 Vi[j] := max(Vi[j], TSm[j]) pour tous j = 1,…N, j  i 2 - Vi[i] := Vi[i] + 1 [0,0,0,0] S1 [0,0,0,0] S2 [0,0,0,0] S3 [0,0,0,0] S4 [1,1,0,0] [2,1,0,0] [3,1,0,0] [3,4,3,1] [0,1,0,0] [0,2,0,0] [3,3,0,0] [0,0,1,1] [2,1,3,1] [2,1,2,1] [0,0,0,1] [0,0,0,2] Retour

  20. Problème – Difficulté moyenne A B C D

  21. Problème – Difficulté moyenne A M 1 M M 3 4 B M 2 M 6 M 5 C D

  22. Problème – Difficulté moyenne

  23. Problème – Difficulté moyenne • Chaque ordinateur commence avec un compteur à 0 et un vecteur de 4 compteurs à 0. • Les compteurs dans le vecteurs sont ainsi: [a,b,c,d]. • Les opérations sont donc: • A: [0,0,0,0], envoi M1 [1,0,0,0], arrivée M3 [2,0,0,1], envoi M4[3,0,0,1]. • B: [0,0,0,0], arrivée M1 [1,1,0,0], envoi M2 [1,2,0,0], arrivée M5[1,3,1,0], arrivée M6[1,4,1,2]. • C: [0,0,0,0], envoi M5 [0,0,1,0], arrivée M2 [1,2,2,0], arrivée M4[3,2,3,1]. • D: [0,0,0,0], envoi M3 [0,0,0,1], envoi M6 [0,0,0,2]. • Envoi M1 = [1,0,0,0] est avant arrivée M2 = [1,2,2,0], • envoi M3 = [0,0,0,1] concurrent arrivée M5 = [1,3,1,0]. Retour

  24. Exercice N°4 – Chandy-Lamport-1- e12 e14 e15 e16 e11 e13 P1 m3 m4 m2 m1 m5 m6 Mk3 e23 e25 P2 e22 e24 e21 m7 m8 Mk3 P3 e31 e32 e34 e35 e33 EL3 EC 13= .. EC 23 = …

  25. Exercice N°4 – Chandy-Lamport-1- Enregistrer état canal EC31  Vide EC 31 = EC 21 = … EL1 e12 e14 e15 e16 e11 e13 P1 m3 m4 m2 m1 m5 m6 Mk3 e23 e25 P2 e22 e24 e21 m7 m8 Mk3 P3 e31 e32 e34 e35 e33 EL3 EC 13= EC 23 = …

  26. Exercice N°4 – Chandy-Lamport-1- EC 31 = EC 21 = … EL1 e12 e14 e15 e16 e11 e13 P1 m3 m4 m2 m1 EC 12 =  m5 m6 EC 32 = … Mk3 e23 e25 P2 e22 EL2 e24 e21 m7 m8 Mk3 P3 e31 e32 e34 e35 e33 EL3 EC 13= EC 23 = …

  27. Exercice N°4 – Chandy-Lamport-1- EC 31 = EC 21 = … EL1 e12 e14 e15 e16 e11 e13 P1 m3 m4 m2 m1 EC 12 =  m5 m6 EC 32 =m7 Mk3 e23 e25 P2 e22 EL2 e24 e21 m7 m8 Mk3 P3 e31 e32 e34 e35 e33 EL3 EC 13= EC 23 =

  28. Exercice N°4 – Chandy-Lamport-1- EC 31 = EC 21 = EL1 e12 e14 e15 e16 e11 e13 P1 m3 m4 m2 m1 EC 12 =  m5 m6 EC 32 =m7 Mk3 e23 e25 P2 e22 EL2 e24 e21 m7 m8 Mk3 P3 e31 e32 e34 e35 e33 EL3 EC 13= EC 23 = Retour

  29. Exercice : Etat global cohérent d’une application répartie • Solution : • Voir la figure ci-dessous pour un trajet possible du marqueur. • En A : • le processus P1 enregistre son état (état(P1) = 1) • et envoie un marqueur sur tous ses canaux sortants, • ici un marqueur est envoyé vers P2 . • En B : • le processus P2 reçoit un marqueur en provenance du processus P1 . • Comme il n’a pas encore enregistré son état, • il enregistre celui-ci (état(P2 ) = 1), • enregistre l’état du canal de P1 vers P2 à  (vide) ;. • Puis il diffuse en C un marqueur sur tous ses canaux sortants. Ici il envoie le marqueur à P3 • En D : • le processus P3 reçoit un marqueur, • enregistre son état (état(P3) = 0) • et l’état du canal de P2 vers P3 à . • Il diffuse ensuite le marqueur à P1

  30. Exercice : Etat global cohérent d’une application répartie • Solution : • En E : • le processus P1 ayant déjà enregistré son état, • il enregistre l’état du canal de P3 vers P1 • comme la liste des messages reçus depuis l’enregistrement, ici {M3}. • Finalement, l’état enregistré est: [1; ; 0;  ; 0; {M3}] • On remarquera que l’état enregistré n’est pas un état de la trajectoire du processus. Mais en permutant les événements e2,S et e1,R qui sont concurrents, on passerait par l’état enregistré. l’état enregistré : Etat (P1) Canal P3 ->P1 = M3 Etat (P2) Canal P1 ->P2 =  Etat (P3) Canal P2 ->P3 = 

  31. Exercice : Etat global cohérent d’une application répartie A A F F e e e e 1S 1S 1R 1R M1 M1 M3 M3 C C e e e e 2S 2S 2S 2S B B e e 2R 2R M2 M2 M2 M2 E E D D e e e e e e ] ] ] ] 3R 3R 3S 3S 3R 3R q ] ] ] q ] ] ] M3 ] q q q M3 ] ] ] q q q q ; 0; ] q q ; 0; ] q q ; 0; ; 0; ; 0; ; 0; q ; 0; ; 0; ; 0; ; 1; ; 0; ; 1; ; 0; ;1; ; 0; M2 ;1; q M2 q M2 M2 M2 q M2 q M2 M2 M2 q M2 ; 0; q ; 1; ; 0; ; 1; ; 0; ; 0; ; 0; ; 1; ; 1; ; 0; ;1; ; 0; ; 0; ; 1; ; 1; ;1; M1 M1 q M1 q q q M1 q q q q q q q q [1; [1; [1; [1; [0; [1; [1; [1; [1; [1; [1; [1; [0; [1; [1; [1; Observation sur canal entrant (P3 -> P1) P1 MK1 MK3 P2 MK2 P3 enregistrer sont état local (état P3) envoyer marqueur sur P3 -> P1 état canal P2 P3 =  enregistrer sont état local (état P2) envoyer marqueur sur P2 -> P3 état canal P1 P2 =  retour

  32. Annexe

  33. Résumé •  Hypothèse : respect de l’ordre des messages :(canaux FIFO) •  Principe •  Utiliser un message “marqueur” pour séparer “avant” et “après” enregistrement pour chaque processus •  Algorithme (à exécuter par tout processus Pi ) •  Première réception du marqueur (depuis Pj ) • 1) Enregistrer état (Pi ) • 2) Enregistrer état (canal <j, i>) comme vide • 3) Diffuser le marqueur à tous ses voisins (processus vers lequel il a un canal) •  {1-2-3} doit être atomique •  Réceptions suivantes du marqueur (depuis Pk ) • Enregistrer état (canal <k, i>) comme : tous les messages reçus de Pk entre l’enregistrement de état (Pj ) et la réception du marqueur de Pk •  Nécessité de détecter la terminaison (enregistrement de tous les états) et de regrouper l’ensemble des données enregistrées

  34. EXEMPLE DE DETERMINATION D'UN ETAT COHERENT • S2 lance la détermination d'état global et diffuse mk2 • Les 3 événements émission2(mk2), réception1(mk2) et réception3(mk2) déterminent une coupure incohérente. • Les marqueurs mk1 et mk3 permettent : • de forcer la transitivité de la causalité et d'avoir une coupure cohérente. • de noter dans les ECij les messages qui traversent la coupure cohérente.

  35. Exemple 2 autre trace et autre état cohérent

More Related