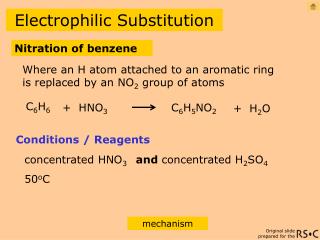
Back Substitution
110 likes | 447 Views
Back Substitution. Matrices Solutions. By Dr. Julia Arnold.

Back Substitution
E N D
Presentation Transcript
Back Substitution Matrices Solutions By Dr. Julia Arnold
In systems that are higher than the 2 dimensional systems you have just studied, it is important to learn how to extend the Gauss-Jordan elimination method to a system with 3 unknowns. However, we do not have to do the entire Gauss-Jordan elimination method in order to obtain a solution. By using a combination of back substitution and Gaussian elimination (to be explained later) we can get a solution for our system with less work. Less work, now that’s an idea!
Consider the following system: x - 2y - 2z = -3 2x + y - z = 7 3x - 2y + 5z = 10 First we convert the system above into a matrix: By Gaussian elimination we end up with a matrix that looks like this: Instead of having zeroes above and below the diagonal We just produce zeroes below the main diagonal.
Consider the following system: x - 2y - 2z = -3 2x + y - z = 7 3x - 2y + 5z = 10 Now let’s learn about back substitution. First we put the variables back and create the equations again. First, notice that our first equation is still the same. Only equations 2 and 3 changed. X - 2y - 2y = -3 5y +3z = 13 z = 1 Now look at equation 3, z = 1. That’s our first solution. By backing up to equation 2 and using the information about z we can find y. 5y + 3(1) = 13 5y = 10 y = 2 Now we know y’s value. Back up to equation 1 to find x’s value. X - 2(2) - 2(1) =-3 x - 4 - 2 = -3 x - 6 = -3 x = 3 X = 3, y = 2, and z = 1 or (3,2,1)
Now you try to find the solution by back substitution: You can put the variables back as you find solutions. For example the correct first step would be to write: 2z = 8 or Y - 4z = 9
Now you try to find the solution by back substitution: You can put the variables back as you find solutions. For example the correct first step would be to write: That’s correct, and thus z = 4. 2z = 8 or Y - 4z = 9
Now you try to find the solution by back substitution: You can put the variables back as you find solutions. For example the correct first step would be to write: 2z = 8 and thus z = 4. Substitute z = 4 into this equation to find y. Y - 4(4) = 9 or y = 25
Now you try to find the solution by back substitution: We know z = 4 and y = 25. How do we find x? 2x +3(25) -1(4) = -5 or 2x +3 - 1 = -5
Now you try to find the solution by back substitution: We know z = 4 and y = 25. How do we find x? That’s correct, and thus x = -38. 2x +3(25) -1(4) = -5 or 2x +3 - 1 = -5
Now that you can back substitute, we now need to learn how to get the matrix in the form we call Gaussian (zeroes below the main diagonal). Zeroes needed here only.
Practice Problems will be found on a separate power point presentation.