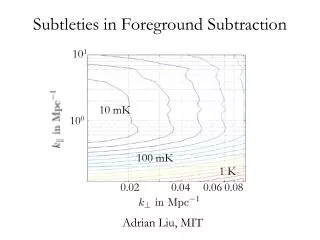
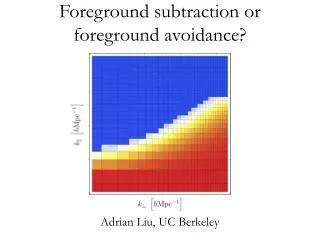
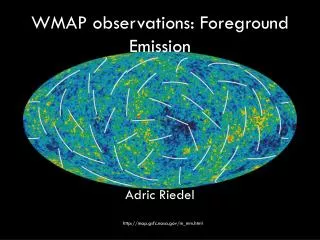
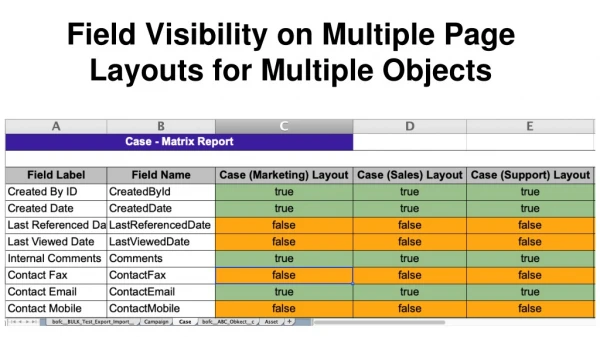
On Multiple Foreground Cosegmentation
380 likes | 605 Views
On Multiple Foreground Cosegmentation. Gunhee Kim Eric P. Xing. School of Computer Science, Carnegie Mellon University. June 18, 2012. Outline. Problem Statement Algorithm Overview Foreground Modeling Region Assignment Experiments Conclusion.

On Multiple Foreground Cosegmentation
E N D
Presentation Transcript
On Multiple Foreground Cosegmentation Gunhee Kim Eric P. Xing School of Computer Science, Carnegie Mellon University June 18, 2012
Outline • Problem Statement • Algorithm • Overview • Foreground Modeling • Region Assignment • Experiments • Conclusion
Image Cosegmentation Jointly segment multiple images into K foregrounds and background High-level signal: recurring objects in multiple images [B11] [J10] [R06] • [R06] Rother et al. CVPR2006 • [H09] Hochbaum and Singh, ICCV2009 • [J10,J12] Joulin et al, CVPR2010,CVPR2012 • [B11] Batra et al, IJCV 2011 • [M11] Mukherjee et al, CVPR 2011 • [V10,V11] Vincente et al, ECCV 2010, CVPR2011 • [K11] Kim et al, ICCV 2011. [K11]
Popular Cosegmentation Datasets CMU-Cornell iCoseg Dataset [Batra et al. IJCV11] MSRC Dataset [Winn et al. ICCV05] Synthesized Dataset [Rhemann et al. CVPR09]
Popular Cosegmentation Datasets CMU-Cornell iCoseg Dataset [Batra et al. IJCV11] Input images are carefully prepared by human so that the objects of interest are salient enough in every single image. MSRC Dataset [Winn et al. ICCV05] Synthesized Dataset [Rhemann et al. CVPR09]
General Users’ Photo Sets A part of Apple+pickingphoto stream from Flickr Girl in red (R)Girl in blue (G) Baby (B) Apple bucket (A) (B,A) (R, G,A) (R, A) (G,A) (R, G,B, A) (R, G,A) (R, G,B, A) (R, A) Follow an ordinary user’s photo-taking pattern. • A series of photos are taken for a specific moment • The number of foregrounds (ie. subjects of interest) are finite • Each image containsanunknown subset of foregrounds
General Users’ Photo Sets A part of Apple+pickingphoto stream from Flickr Girl in red (R)Girl in blue (G) Baby (B) Apple bucket (A) (B,A) (R, G,A) (R, A) (G,A) Has NOT yet explicitly addressed (R, G,B, A) (R, G,A) (R, G,B, A) (R, A) Follows an ordinary users’ photo-taking pattern. • A series of photos are taken for a specific moment • The number of foregrounds (ie. subjects of interest) are finite • Each image containsanunknown subset of foregrounds
Problem StatementMultiple Foreground Cosegmentation Girl in red (R)Girl in blue (G) Baby (B) Apple bucket (A) (B,A) (R, G,A) (R, A) (G,A) (R, G,B, A) (R, G,A) (R, G,B, A) (R, A) Given an image setI, K foregrounds of interest Segment each image into regions of {F1,…,FK+1} (FK+1=B) • Optionally, a user may assign some examples of foregrounds. • Each image containsanunknown subset of foregrounds
Outline • Problem Statement • Algorithm • Overview • Foreground Modeling • Region Assignment • Experiments • Conclusion
Overview of Algorithm Supervised Iteratively solve Assigned by a user Initialization Unsupervised Apply diversity ranking of [Kim et al. ICCV11] ✔ RegionAssignment Foreground Modeling • Performed in each image separately • Allocate the regions of image into one of K+1 FGs • Learn appearance models of K+1 foregrounds (FGs) Iterate until convergence [Kim&ToralbaNIPS09] [Rother et al. SIGGRAPH04]
Outline • Problem Statement • Algorithm • Overview • Foreground Modeling • Region Assignment • Experiments • Conclusion
Foreground (FG) Model Baby FG model Baby FG model Definition of k-th FG model A parametric function Given any region S, return its value (score) of FG k Any region classifiers or their combination Value Assignment (Testing) Foreground learning (Training)
Foreground (FG) Model Definition of k-th FG model A parametric function Given any region S, return its value (score) to FG k Any region classifiers or their combination Gaussian Mixture Model (GMM) Spatial Pyramid + linear SVM (SPM) • One of most popular in cosegmentation literatures • One of most popular in image classification • RGB colors • Gray/HSV SIFT
Outline • Problem Statement • Proposed Algorithm • Foreground Modeling • Region Assignment • Experiments • Conclusion
Region Assignment Given learned (or initialized) FG Models, RA is individually performed in each image Person FG Cow FG Oversegment Background
Region Assignment Given learned (or initialized) FG Models, RA is individually performed in each image Person FG Cow FG Background Region Assignment
A NaïveRegion Assignment A naïve way: Assign each segment to the FG whose value is the highest Person FG Cow FG Background Cow BG BG BG Cow However, it will NOT work !
Why does not A NaïveRA work? Most naïve way: Assign each segment to FG whose value is the highest s1 Cow won! Person FG Cow FG Person won! s2 My value of {s1,s2} is 18. My value of s2 is 5. My value of s1 is 10. My value of {s1,s2} is 35. My value of s2 is 20. My value of s1 is 7. {s1,s2}
Why does not A NaïveRA work? Most naïve way: Assign each segment to FG whose value is the highest Value of {s1,s2}to person FG Value of s1 to CowFG Value of s2 to person FG > s1 + Cow won! Person FG Cow FG Have to evaluate the combinations of segments Person won! s2 My value of {s1,s2} is 35. My value of s2 is 20. My value of s1 is 7. My value of {s1,s2} is 18. My value of s1 is 10. My value of s2 is 5. {s1,s2}
Region Assignment by Combinatorial Auction Bidder 2 Bidder 1 (or buyer) Person FG Cow FG Items to sell Bidder 3 Background • Each FG is allowed to bid packagesof items with their own values. • Distribute the segments to maximize the values.
RegionAssignment as Combinatorial Auction Assign the segments to FGs to maximize the overall values. Feasibility: Each segment cannotbe assigned more than once |Si| 2 Unfortunately, NP-complete and Inapproximable Winner determination problem (ie. Welfare maximization) subsets [Cramton et al. 2005].
Next Goal: Tractable Solution to WDP There are two different ways… 1. Constraints on value functions • If value functions are submodular or subadditive, … ✔ 2. Constraints on generating bidding packages Allow any combinations of FG models (ie. Regionclassifiers) [Felzenszwalb et al.2008]
Procedure of Region Assignment Follow a general combinatorial auction scenario. 1. Each FG creates a set of foreground candidates : n FG candidates by FG k • : a bundle of segments • : its value : FG ID • In this step, each FG does not care their winning chances. 2. Finally, 3. Solve WDP by choosing feasible FG candidates.
Assumption for FG Candidates A FG instance in an image = a set of adjacentsegments. A FG instance = a sub-tree of Gi Any FG candidate = a sub-tree of Gi
Generating FG Candidatesby Beam Search For each size of candidates, we keep only D high valued ones. 1. Oevery single segment For each foreground k, 2. Otall possible subgraphs by adding a single edge to elements of O. 3. Compute values vovk(o)for all and keep only top D high valued ones to O. 4. Iterate (|Si|-1) times. • Beam width D • Computation time: O(D|Si|2) • Number of FG candidates per FG: |Bik| = O(D|Si|)
Example of Candidate Set Apple bucket 18.78 19.74 29.30 39.42 Baby 16.35 18.22 39.47 47.06 Back-ground 19.88 19.85 39.61 59.49
Solving WDP The number of FG candidates is (K+1)D|Si|. By search in polynomial time Even a faster algorithm… Apple bucket 18.78 19.74 29.30 39.42 Solve WDP ! Baby 16.35 18.22 39.47 47.06 Back-ground 19.88 19.85 39.61 59.49
Solving WDP [Theorem] Dynamic program can solve WDP in O(|Bi||Si|) worst time if every candidate in Bi can be represented by a connected subgraph of a tree Ti*. [Sandholm et al.2003] Each FG candidate is a tree, but the aggregation is not. Apple bucket 18.78 19.74 29.30 39.42 Candidate 1 Baby 39.47 47.06 16.35 18.22 Candidate 2 Back-ground 19.88 19.85 39.61 59.49
Inferring the Most Probable Tree from FG Candidate Set Solve the following MLE solution where : all possible spanning trees Reject the bids that are not a subtree of Apple bucket w1 = 20 18.78 19.74 29.30 39.42 Candidate 1 Baby 39.47 47.06 16.35 18.22 Candidate 2 Back-ground w2 = 5 19.88 19.85 39.61 59.49
Inferring the Most Probable Tree from Candidate Set Solve the following MLE solution where : all possible spanning trees Almost identical to Chow-Liu tree structure learning Apple bucket 18.78 19.74 29.30 39.42 MLE solution = MST by Kruskal’salgorithm in O(|Bi||Si|2) Baby 39.47 47.06 16.35 18.22 Back-ground 19.88 19.85 39.61 59.49
Finally, Solve WDP [Theorem] Dynamic program can solve WDP in O(|Bi||Si|) worst time if every candidate in Bi can be represented by a connected subgraph of a tree Ti*. [Sandholm et al.2003] CABOB algorithm [Sandholm et al.2005] segmentation optimal assignment
Outline • Problem Statement • Proposed Algorithm • Foreground Modeling • Region Assignment • Experiments • Conclusion
Two Experiments FlickrMFC dataset • Goal: To achieve multiple foreground cosegmentation • Goal: Scalability • New benchmark dataset (14 groups, 20 images, fully-labeled) ex. Cow group: {person, car, cow (brown, black)} ImageNet dataset ex. green lizard
Quantitative Evaluation Segmentation accuracies Metric MFC-S: (supervised) our method MFC-U: (unsupervised) our method COS : Submodular optimization [Kim et al. ICCV11] DC: Discriminative clustering [Joulin. CVPR10] LDA: LDA-based localization [Russell et al. CVPR06] MNcut: Normalized cuts [Cour et al. CVPR05]
Cosegmentation Examples FlickrMFC ImageNet Lion Australian terrier
Outline • Problem Statement • Proposed Algorithm • Foreground Modeling • Region Assignment • Experiments • Conclusion
Conclusion Multiple foreground cosegmentation • Each image contains aunknown subset of foregrounds • Web-oriented applications • Code and FlickrMFCdataset will be available in this month! Combinatorial auction-based region assignment • Fast and distributable (ex. Linear with M,K, polynomial in |Si|) • Can be used for other tasks (ex.detection) beyond segmentation.
Take-Home Message Combinatorial optimization for Image Segmentation! • New region descriptors & classifiers every year • Multiple fast machines are available. May avoid difficult ML algorithmsor high-order models Similar line of thought: Our ICCV 2011 paper Simply enumerate the cases (or hypotheses) not in a brute-force but in a smartway. Submodular optimization