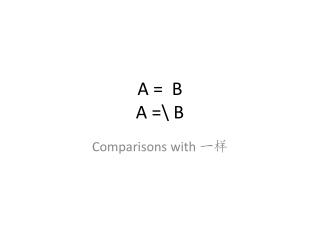BÉZIEROVE KRIVE
210 likes | 454 Views
Miloš Novković Nikola Ristovski Uroš Stegić Željko Jovanović. BÉZIEROVE KRIVE. OPIS BÉZIEROVE KRIVE. Označimo sa P skup određenih tačaka u ravni; P = {P 1 , P 2 , ... , P n } Bezierova kriva je zadata sa:. CRTANJE BÉZIEROVE KRIVE. Algoritam aproksimacija(Tacka *ktacke, int n)

BÉZIEROVE KRIVE
E N D
Presentation Transcript
Miloš Novković Nikola Ristovski Uroš Stegić Željko Jovanović BÉZIEROVE KRIVE
OPIS BÉZIEROVE KRIVE • Označimo sa P skup određenih tačaka u ravni; P = {P1, P2, ... , Pn} • Bezierova kriva je zadata sa:
CRTANJE BÉZIEROVE KRIVE Algoritam aproksimacija(Tacka *ktacke, int n) Ulaz: kontrolne tačke smeštene u niz (Tacka *ktacke), dimenzija niza (int n); Izlaz: niz tačaka, dimenzije 1000, koji predstavlja aproksimaciju Bezierove krive (Tacka *P). begin P[0] = ktacke[0] koef = 0.001 lambda = koef
CRTANJE BÉZIEROVE KRIVE i = 0 while i < 1000 do while j < n do niz[j] = ktacke[j] P[i] = deCasteljau(niz, n, lambda) i++ lambda += koef return P end
CRTANJE BÉZIEROVE KRIVE AlgoritamdeCasteljau(Tacka *ktacke, int n, float l) Ulaz: niz kontrolnih tačaka, njegova dimenzija, preciznost aproksimacije; Izlaz: Tačka dobijena nakon n-2 iteracije algoritma deCasteljau. begin if(n == 2) Tacka q Tacka AB AB.x = ktacke[1].x - ktacke[0].x AB.y = ktacke[1].y - ktacke[0].y MnozenjeSkalarom(AB,l,&q) ZbirVektora(ktacke[0],q,&q) return q
CRTANJE BÉZIEROVE KRIVE else i = 0 while i<n-1 do AB.x = ktacke[i+1].x - ktacke[i].x AB.y = ktacke[i+1].y - ktacke[i].y MnozenjeSkalarom(AB,l,&q) ZbirVektora(ktacke[i],q,&q) P[i] = q i++ return deCasteljau(P,n-1,l) end
PROMENA STEPENA KRIVE AlgoritamPovecajStepen(Tacka* ktacke, int n, int m, Tacka* niz) Ulaz: niz kontrolnih tačaka, njegova dimenzija, stepen povećanja i novi niz; Izlaz: popunjen niz niz. begin i = 0 kopiranje niza ktacke u niz niz i = 0 while i<m do Stepen(niz,n+1) end
PROMENA STEPENA KRIVE Prva i zadnja (n-та) tačka u nizu ostaju iste jer se oblik krive ne menja. Od ostalih n-2 tačaka treba napraviti n-1, odnosno povećati stepen krive za jedan. Svaka od tih tačaka se određuje pomoću formule:
PROMENA STEPENA KRIVE Algoritam Stepen(Tacka* niz, int n) Ulaz: niz kontrolnih tačaka kome treba dodati još jednu tačku, dimenziju niza; Izlaz: niz sa dodatom jednom tačkom. begin //proširivanje niza za jedan niz[n] = niz[n-1] i = n-1
PROMENA STEPENA KRIVE while i>0 do l, h - tacke float w = (1.0 * i) / (n+1) float v = 1 - ((1.0 * 1) / (n+1)) MnozenjeSkalarom(niz[i-1], w, &l) MnozenjeSkalarom(niz[i], v, &h) niz[i].x = l.x + h.x noz[i].y = l.y + h.y end Složenost funkcije je О(m * n).
PODELA KRIVE Algoritam sadrži sledeće korake: 1) Prva kontrolna tačka krive takođe je i prva kontrolna tačka nove krive, kao i da je zadnja kontrolna tačka krive zadnja kontrolna tačka druge krive. 2) Izračunamo vektor od prve do druge kontrolne tačke, uzmemo njegovu polovinu i dodamo na prvu tačku.Rezultat je nova tačka. AB.x = ktacke[i+1].x - ktacke[i].x AB.y = ktacke[i+1].y - ktacke[i].y MnozenjeSkalarom(AB,l,&q) ZbirVektora(ktacke[i],q,&q)
PODELA KRIVE 3) Ponavljamo korak 2) dok ne prođemo kroz sve tačke. 4) Ponavljamo korake 2) i 3) i svakim ponavljanjem imaćemo po jedan vektor manje. Ponavljanje se vrši dok ne dobijemo samo dve tačke, tj. Jedan vektor, odredimo njegovu polovinu i ta tačka predstavlja traženu tačku koja deli početnu Bezierovu krivu na dva jednaka dela.
PODELA KRIVE Prvi set kontrolnih tačaka za prvu polovinu krive predstavljaju tačke dobijene u prvom deljenju vektora pri svakom od n deljenja, tako da su kontrolne tačke prve polovine krivine (po oznakama na slici) 00, 10, 20, 30, 40, 50, 60. Dalje primetimo da su kontrolne tačke druge krive dobijene pri svakom deljenju trenutnog poslednje vektora pri svakom od n deljenja tako da su kontrolne tačke druge polovine krive (po oznakama na slici) 60, 51, 42, 33, 24, 15, 06. Kao što možemo primetiti tačka koja se nalazi na sredini ili (po slici) 60 pripada obema krivima.
APROKSIMACIJA Krivu možemo aproksimirati na dva načina: • Koristeći formulu iz definicije • De Casteljau-ovim algoritmom
UPOTREBA Najčešća mesta gde se sreću krive: • Fontovi • Vektorska grafika • Animacije