1 / 19

Exploring Ganglion Cell Responses and Receptive Fields in Visual Processing

This study investigates the response of on-center ganglion cells in the Limulus eye to various stimuli, highlighting mechanisms like lateral inhibition and local contrast. Using mathematical functions to model firing rates based on luminance and contrast, the analysis explores how ganglion cells behave under different visual conditions. Adaptation effects and the response invariance to illumination changes are examined, particularly focusing on sine wave gratings to understand how receptive fields influence firing rates across various frequencies.

dawn-mack
Download Presentation

Exploring Ganglion Cell Responses and Receptive Fields in Visual Processing

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

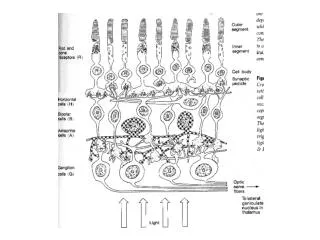
  1. Hartline Experiment • Limulus eye has ommotidia containing one receptor each. • Each receptor sends a large axon to the brain. • Output of one receptor was inhibited by light shining on a neighboring receptor (lateral inhibition).

  2. Ganglion cell receptive fields • Receptive field - region of visual field that cell responds to. • Center-surround receptive field On-center, off-surround Off-center, on-surround - - - + + - - - - + + - + - + - + - - + - + + - - + + - - - + + - + - - - + - - - - + - - - + +

  3. Problem • Plot the response of an array of on-center ganglion cells to this image. - - - - - - + + - - - - Ganglion cells

  4. Ganglion cells as computational devices • Write a mathematical function that calculates firing rate of cell from luminance pattern. • 1st guess • Increase in firing rate = weighted sum of intensities within receptive field. • Problem 1 - Adaptation • Problem 2 - dark regions in inhibitory region actually excite cell

  5. Ganglion cells as computational devices • Solution • Increase in firing rate = weighted sum of local contrast values within receptive field. • Local contrast C(x,y) = I(x,y) / M - 1

  6. Ganglion cells as computational devices • Solution • Increase in firing rate = weighted sum of local contrast values within receptive field. • Local contrast C(x,y) = I(x,y) / M - 1 Intensity

  7. Ganglion cells as computational devices • Solution • Increase in firing rate = weighted sum of local contrast values within receptive field. • Local contrast C(x,y) = I(x,y) / M - 1 Mean intensity Intensity

  8. Ganglion cells as computational devices • Solution • Increase in firing rate = weighted sum of local contrast values within receptive field. • Local contrast C(x,y) = I(x,y) / M - 1 Mean intensity Intensity Local contrast

  9. Intensity Contrast

  10. Is firing rate of on-center ganglion cell above or below resting level? 3 2 1

  11. Contrast coding • Response of ganglion cells is invariant to changes in illumination level • This breaks down at extremes (e.g. at night)

  12. - + - - Experiment: What is the response of a ganglion cell To a sine wave grating?

  13. - + - - Ganglion cell receptive field 1 cycle / deg. 2 cycles / deg. 4 cycles / deg. 8 cycles / deg. 16 cycles / deg. Assume: A bright bar of a grating is centered in receptive field. Plot the firing rate of this cell as a function of grating frequency.

  14. - + - - Simple cell receptive field - 1 cycle / deg. 2 cycles / deg. 4 cycles / deg. 8 cycles / deg. 16 cycles / deg. Plot firing rate of cell as a function of grating frequency

More Related