exercise in the previous class
290 likes | 452 Views
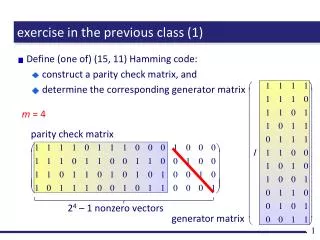
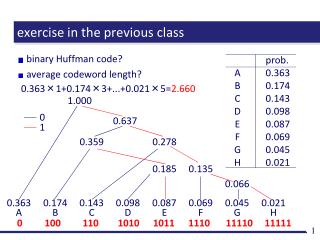
exercise in the previous class. Write a computer program to construct a Huffman code... typical application of the data structure “ priority queue ” a collection of data with each associated with “ priority ” enqueue : add a data in the collection

exercise in the previous class
E N D
Presentation Transcript
exercise in the previous class Write a computer program to construct a Huffman code... typical application of the data structure “priority queue” • a collection of data with each associated with “priority” • enqueue: add a data in the collection • dequeue: retrieve a data with the largest priority • tree = data, smaller probability = higher priority • dequeue two trees, join them, and enqueue the result • at the final satge, give labels to the unified single tree 0.3 enqueue dequeue 0.1 0.2 0.3 0.4
review of the previous class • Shannon’s source coding theorem • the average codeword length is H(S) or more • the length can be reduced to H(S) + ε for any ε • “block” version of Huffman codes • encode by block, and we have more compact coding • there are various approaches to define block patterns there is an additional remark concerning the block coding
handling the “tail” of the data block coding cannot be applied if... • the message is too short • we have leftover symbols • the last run is not terminated • no clever solution, get around problems by operational devises • use different coding for the final (leftover) block • use padding, etc.
today’s class some more source coding scheme • coding for “simple” realization • arithmetic codes • coding for the unknown information sources • Lempel-Ziv algorithms • coding which sacrifices the uniquely decodable property • non-reversible, or lossy, coding
arithmetic code part I • coding for “simple” realization
realization issue of coding • coding ≈ translation between symbols and codewords • We need a large translation table to obtain good performance. • static (静的な) approach... • construct the table beforehand, and keep it in the system • the translation is made by a simple table-lookup • large memory is needed not good for realization • dynamic (動的な) approach... • the table is not constructed explicitly (明示的に) • the table-lookup is replaced by on-the-fly computation
S(wi) 0 0.343 0.490 0.637 0.700 0.847 0.910 0.973 arithmetic code arithmetic code...well-known example of the dynamic approach • the idea is sketched by an example: • p(A) = p, p(B) = 1 – p, the block size is n • in numerical examples, we use p= 0.7 and n = 3 i 0 1 2 3 4 5 6 7 wi AAA AAB ABA ABB BAA BAB BBA BBB P(wi) 0.343 0.147 0.147 0.063 0.147 0.063 0.063 0.027 We have 23 = 8 block patterns. • w0, ..., w7, in the dictionary order • : probability that wi occurs (sum of probabilities beforewi)
S(wi) 0 0.343 0.490 0.637 0.700 0.847 0.910 0.973 illustration of probabilities • the eight patterns partition the interval [0, 1]; 0 0.5 1.0 AAA AAB ABA ABB BAA BAB BBA BBB 0.343 0.147 0.147 0.063 0.147 0.063 0.063 0.027 S(ABB) S(BAA) = S(ABB)+P(ABB) i 0 1 2 3 4 5 6 7 wi AAA AAB ABA ABB BAA BAB BBA BBB P(wi) 0.343 0.147 0.147 0.063 0.147 0.063 0.063 0.027 • wi occupies the interval basic idea: • encode wias a certain value problem to solve: • need a translation between wi and
A B AA AB BA AB AAA AAB ABA ABB BAA BAB BAB BBB 0.027 0.343 0.147 0.147 0.063 0.147 0.063 0.063 about the translation two directions of the translation: • [encode] the translation from wi to • [decode] the translation from to wi ...use recursive computation instead of a static table P(w) S(w) P(wA) P(wB) S(wA) S(wB)
[encode] the translation from wi to • recursively determine P( ) and S( ) for prefixes of wi • P(ε) = 1, A(ε) = 1 • for a pattern wA, P(wA) = P(w)p, S(wA) = S(w) • for a pattern wB, P(wB) = P(w)(1 – p), S(wB) = S(w) + P(w)p the interval of “ABB” ? P(w) P() = 1 S() = 0 S(w) P(A)=0.7 S(A) = 0 P(wA) P(wB) A B S(wA) S(wB) AB P(AB)=0.21 S(AB) = 0.49 AA the interval of “ABB” is [0.637, 0.637 + 0.063) ABA ABB P(ABB)=0.063 S(ABB) = 0.637 p = P(A) = 0.7
[encode] the translation from wi to (cnt’d) Given a pattern wi, now we know the interval , but which should be chosen? • we want whose binary representation is the shortest. • choose as S(wi) + P(wi) but trimming at places (...以下を切り捨て) S(wj) + P(wj) S(wj+1) 0.aa...aaa...a +0.00...0bb...b 0.aa...acc...c 0.aa...ac0...0 the length of x ≈ – log2P(wi) place (桁数) of the most significant non-zero of P(wj) x = – log2P(wj) 0.aa...ac 0.aa...aaa...a 0.aa...acc...c
[decode] the translation from to wi goal: given x, determine the leaf node whose interval contains x • almost the same as the first half of the encoding translation • compute, compare, and move to the left or right x = 0.600 P() = 1 S() = 0 P(w) A(w) P(A)=0.7 S(A) = 0 A B S(B) = 0.7 P(wA) P(wB) AA AB P(AB)=0.21 S(AB) = 0.49 threshold A(wA) A(wB) ABA ABB P(ABA)=0.147 S(ABA) = 0.49 S(ABB) = 0.637 0.600 is contained in the interval of ABA...decoding completed
performance, summary an n-symbol pattern w with probability P(w) encoded to a sequence with length • the average codeword length per symbol is • almost optimum coding without using a translation table however... • we need much computation with good precision ( use approximation?)
Lempel-Ziv algorithms part II • coding for the unknown information sources
probability in advance? so far, we assumed that the probabilities of symbols are known... in the real world... • the symbol probabilities are often not known in advance • scan the data twice? • first scan...count the number of symbol occurrences (出現) • second scan...Huffman coding • delay of the encoding operation? • overhead to transmit the translation table?
Lempel-Ziv algorithms for information sources whose symbol probability is not known... • LZ77 • lha, gzip, zip, zoo, etc. • LZ78 • compress, arc, stuffit, etc. • LZW • GIF, TIFF, etc. work fine for any information sources universal coding (ユニバーサル符号化)
LZ77 L • proposed by A. Lempel and J. Zivin 1977 • represent a data substring by using a substring which has been occurred previously algorithm overview • process the data from the beginning • partition the data to blocks in a dynamic manner • represent a block by a three-tuple(i, l, x) • “rewind i symbols, copy l symbols, and append x” Z x –i –i+l –1 0 l–1 l encoding completed
encoding example of LZ77 • consider to encode ABCBCDBDCBCD symbol A B C B C D B D C B C D history first time first time first time = (here) – 2 = (here) – 2 ≠ (here) – 2 = (here) – 3 ≠ (here) – 3 = (here) – 6 = (here) – 6 = (here) – 6 = (here) – 6 codeword (0, 0, A) (0, 0, B) (0, 0, C) (2, 2, D) (3, 1, D) (6, 4, *)
decoding example of LZ77 • decode (0, 0, A), (0, 0, B), (0, 0, C), (2, 2, D), (3, 1, D), (6, 4, *) possible problem: • large block is good, because we can copy more symbols • large block is bad, because a codeword contains a large integer ... the dilemma degrades the performance.
x –b –1 0 encoding completed LZ78 • proposed by A. Lempel and J. Ziv in 1978 • represent a block by a thw-tuple(b, x) • “copy the b-thblock before, and append x”
encoding example of LZ78 • consider to encode ABCBCBCDBCDE symbol A B C B C B C D B C D E history first time first time first time = (here) – 2 block = (here) – 1 block = (here) – 1 block codeword (0, A) (0, B) (0, C) (2, C) (1, D) (1, E) block # 1 2 3 4 5 6
decoding example of LZ78 • decode (0, A), (0, B), (0, C), (2, C), (1, D), (1, E) advantage against LZ77: • large block is good, because we can copy more symbols • is there anything wrong with large blocks? the performance slightly better than LZ78
summary of LZ algorithms in LZ algorithms, the translation table is constructed adoptively • information sources with unknown symbol probabilities • information sources with memory • LZW: good material to learn intellectual property (知的財産) • UNISYS, CompuServe, GIF format, ...
non-reversible, or lossy, coding part III • coding which sacrifices the uniquely decodable property
uniquely decodable? really needed? We have considered codes which are uniquely decodable. • “encode, decode, and we have the original data” • reversible code, lossless code (可逆,無歪み符号) Sometimes, the uniquely decodable property is too much. • image, sound, etc...OK if similar to the original • non-reversiblecode, lossycode(非可逆,有歪み符号) • more compactness individual coding schemes are not given in this lecture...
Shannon’s theorem, reconsidered • Shannon’s source coding theorem: • for any code, the average codeword length ≥ H(X) • a code with average codeword length <H(X) + ε is constructible • encoder = communication channel • input X = symbol(s), output Y = codeword(s) • reversible: the knowledge of Y uniquely determines X • entropies: H(X) → 0 ... mutual information I(X; Y) = H(X) “A codeword is a container of the information with size I(X; Y).” ... A codeword cannot be smaller than H(X). X? X Y encoder
non-reversible case non-reversible code: • the knowledge of Ydoes not eliminate all ambiguity on X • “AFTER entropy” > 0, mutual information I(X; Y) < H(X). “A codeword is a container of the information with size I(X; Y).” • it can happen that the average codeword length < H(X) • “a code beyond Shannon’s theorem” may exist. the theory is more complicated, cf. rate-distortion theorem X? X Y encoder
summary of today’s talk source coding other than Huffman codes • coding for “simple” realization • arithmetic codes • coding for the unknown information sources • Lempel-Ziv algorithms • coding which sacrifices the uniquely decodable property • non-reversible, or lossy, coding
exercise • Encode ABACABADACABAD by the LZ77 algorithm, and decode its result. • Survey what has happened concerning the patent of LZW.