Sliding window protocol
260 likes | 1.93k Views
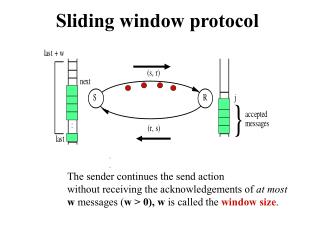
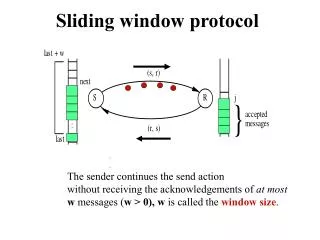
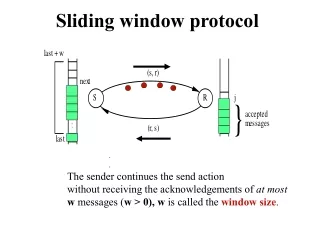
Sliding window protocol. The sender continues the send action without receiving the acknowledgements of at most w messages ( w > 0), w is called the window size . . {program for process S} define next, last, w : integer ; initially next = 0, last = -1, w > 0

Sliding window protocol
E N D
Presentation Transcript
Sliding window protocol • The sender continues the send action • without receiving the acknowledgements of at most • w messages (w > 0), w is called the window size.
{program for process S} define next, last, w : integer; initially next = 0, last = -1, w > 0 do last+1 ≤ next ≤ last + w send (m[next], next); next := next + 1 (ack, j) is received if j > last last := j j ≤ last skip fi timeout (R,S) next := last+1 {retransmission begins} od {program for process R} define j : integer; initially j = 0; do (m[next], next) is received if j = next accept message; send (ack, j); j:= j+1 j ≠ next send (ack, j-1) fi; od Sliding window protocol
Why does it work? Lemma. Every message is accepted exactly once. Lemma. m[k] is always accepted before m[k+1]. (Argue that these are true.) Observation. Uses unbounded sequence number. This is bad. Can we avoid it?
Theorem If the communication channels are non-FIFO, and the message propagation delays are arbitrarily large, then using bounded sequence numbers, it is impossible to design a window protocol that can withstand the (1) loss, (2) duplication, and (3) reordering of messages.
Why unbounded sequence no? (m’’,k) (m’, k) (m[k],k) New message using the same seq number k Retransmitted version of m We want to accept m” but reject m’. How is that possible?
Alternating Bit Protocol m[2],0 m[1],1 m[0],0 m[0],0 R S ack, 0 ABP is a link layer protocol. Works on FIFO channels only. Guarantees reliable message delivery with a 1-bit sequence number (this is thetraditional version with window size = 1). Study how this works.
Alternating Bit Protocol programABP; {program for process S} define sent, b : 0 or 1; next : integer; initially next = 0, sent = 1, b = 0, and channels are empty; do sent ≠b send (m[next], b); next := next+1; sent := b (ack, j) is received if j = b b := 1-b j ≠ b skip fi timeout (R,S) send (m[next-1], b) od {program for process R} define j : 0 or 1; {initially j = 0}; do (m[ ], b) is received if j = b accept the message; send (ack, j); j:= 1 - j j ≠ b send (ack, 1-j) fi od S m[2],0 m[1],1 a,0 m[0],0 m[0],0 R
How TCP works Supports end-to-end logical connectionbetween any two computers on the Internet. Basic idea is the same as those of sliding window protocols. But TCP uses bounded sequence numbers! It is safe to re-use a sequence number when it is unique. With a high probability, a random 32 or 64-bit number is unique. Also, current sequence numbers are flushed out of the system after a time = 2d, where d is the round trip delay.
How TCP works • Three-way handshake. Sequence numbers are unique w.h.p. • Why is the knowledge of roundtrip delay important? • What if the window is too small / too large? • What if the timeout period is too small / too large? • Adaptive retransmission: receiver can throttle sender • and control the window size to save its buffer space.
Distributed Consensus Reaching agreement is a fundamental problem in distributed computing. Some examples are Leader election / Mutual Exclusion Commit or Abort in distributed transactions Reaching agreement about which process has failed Clock phase synchronization Air traffic control system: all aircrafts must have the same view If there is no failure, then reaching consensus is trivial. All-to-all broadcast Followed by a applying a choice function … Consensus in presence of failures can however be complex.
Problem Specification output input v u0 p0 v u1 p1 u2 p2 v p3 u3 v Here, v must be equal to the value at some input line. Also, all outputs must be identical.
Problem Specification Termination. Every non-faulty process must eventually decide. Agreement. The final decision of every non-faulty process must be identical. Validity. If every non-faulty process begins with the same initial value v, then their final decision must be v.
Asynchronous Consensus Seven members of a busy household decided to hire a cook, since they do not have time to prepare their own food. Each member separately interviewed every applicant for the cook’s position. Depending on how it went, each member voted "yes" (means “hire”) or "no" (means “don't hire”). These members will now have to communicate with one another to reach a uniform final decision about whether the applicant will be hired. The process will be repeated with the next applicant, until someone is hired. Consider various modes of communication…
Asynchronous Consensus Theorem. In a purely asynchronous distributed system, the consensus problem is impossible to solve if even a single process crashes Famous result due to Fischer, Lynch, Patterson (commonly known as FLP 85)
Proof Bivalent and Univalent states A decision state is bivalent, if starting from that state, there exist two distinct executions leading to two distinct decision values 0 or 1. Otherwise it isunivalent. A univalent state may beeither 0-valent or 1-valent.
Proof Lemma. No execution can lead from a 0-valent to a 1-valent state or vice versa. Proof. Follows from the definition of 0-valent and 1-valent states.
Proof Lemma. Every consensus protocol must have a bivalent initial state. Proof by contradiction.Suppose not. Then consider the following input patterns: s[0]0 0 0 0 0 0 …0 0 0 {0-valent) 0 0 0 0 0 0 …0 0 1 s[j] is 0-valent 0 0 0 0 0 0 …0 1 1 s[j+1] is 1-valent … … … … (differ in jth position) s[n-1] 1 1 1 1 1 1 …1 1 1 {1-valent} What if process (j+1) crashes at the first step?
Lemma. In a consensus protocol, starting from any initial bivalent state, there must exist a reachable bivalent stateT, such that every action taken by some process p in state T leads to either a 0-valent or a 1-valent state. Proof The adversary tries to prevent The system from reaching consensus Actions 0 and 1 from T must be taken by the same process p. Why?