Character Tables
260 likes | 857 Views
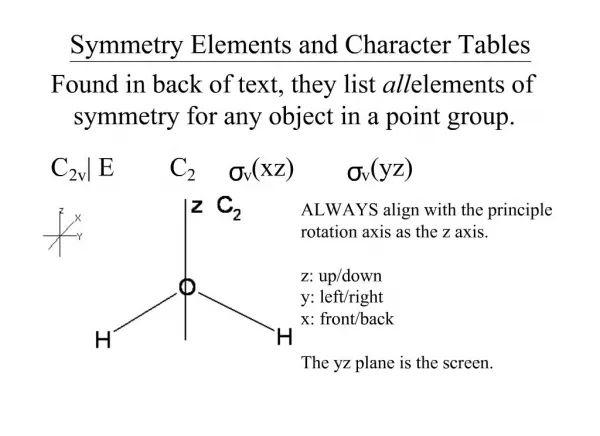
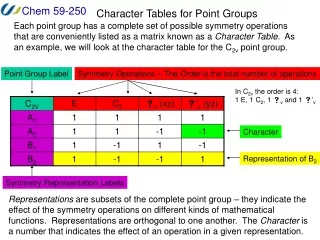
Karakter Çizelgesi. Character Tables. Character Tables. Each point group has a complete set of possible symmetry operations that are conveniently listed as a matrix known as a Character Table . . Point Group Label. Symmetry Operations – The Order is the total number of operations.

Character Tables
E N D
Presentation Transcript
Karakter Çizelgesi Character Tables
Character Tables Each point group has a complete set of possible symmetry operations that are conveniently listed as a matrix known as a Character Table. Point Group Label Symmetry Operations – The Order is the total number of operations In C2v the order is 4: 1 E, 1 C2, 1 v and 1 ’v Character Symmetry Representation Labels 4 characters: İrreducible represention of B2
Karakter Çizelgesi s C E 2 C 3 3 3 v v 1 1 1 A1 - 1 1 1 A2 - 2 1 0 E Simetri işlemleri s s s 2 C E C C ' ' ' 3 3 3 v v v v G 1 1 1 1 1 1 1 İndirgenemez gösterimler (İG) Irreducible representations (IR) G - - - 1 1 1 1 1 1 2 G - - 2 1 1 0 0 0 3 3 sınıf mevcuttur Grup derecesih= 6 (h = 1 +2 +3) Eşdeğer elemanlar ve eşdeğer atomlar sınıf oluşturur. Mulliken Sembolleri
Mulliken Sembolleri A baş dönme eksenine göre simetrik (+) B baş dönme eksenine göre antisimetrik (−) A veya B tek boyutlu İG E iki boyutlu İG T ( veya F)üç boyutlu İG Altindis 1 C2 ( Cn) eksenine, yoksa v işlemine göre simetrik ( = +1) 2 C2 ( Cn) eksenine, yoksa v işlemine göre antisimetrik ( = -1) Alt indis g(gerade)evirme işlemine göre simetrik ( = +1) u(ungerade) evirme işlemine göre antisimetrik ( = −1) Üst indis ' (tek üs)h düzlemine göre simetrik (+) ''(çift üs)“antisimetrik (−)
Karakter Çizelgeleri ve Mulliken Sembolleri-1 • C1 group. Consists of a single operation E; thus its order h=1 and number of classes is 1. There is a single irreducible representation. • Cs group. Consists of two operations, E andsh; thus its order h is 2 and the number of classes is 2. There are two irreducible representations. • Ci group. Consists of two operations, E and i. Both its order h and number of classes is 2. Similarly to Cs, the group includes two irreducible one-dimensional representations.
Karakter Çizelgeleri ve Mulliken Sembolleri-2 ÖRNEK: C2v ve C3v nokta gruplarının karakter çizelgelerindeki Mulliken sembollerini belirleyiniz. C2v E C2sxzsyz A1+1+1 +1 +1 Tz A2+1+1-1 -1 Rz B1 +1 -1+1 -1 Tx or Ry B2 +1 -1-1 +1 Ty or Rx C3v E 2C3 3sv A1+1+1+1 Tz A2+1+1-1 Rz E+2 -1 0 (Tx, Ty) or (Rx, Ry)
s s C E 2 C C 2 2 4 4 2 v v d + 2 2 2 A 1 1 1 1 1 z x y , z 1 - - A 1 1 1 1 1 R 2 z - - - 2 2 B 1 1 1 1 1 x y 1 - - B 1 1 1 1 1 xy 2 E 2 0 0 0 ( x , y ), ( R , R ) ( xz , yz ) - 2 x y İkili fonksiyonlar ( d orbitalleri) Tekli fonksiyonlar (p orbitalleri) Karakter Çizelgeleri ve Mulliken Sembolleri-3 C4vnokta grubunun tam karakter çizelgesi These are basis functions for the irreducible representations. They have the same symmetry properties as the atomic orbitals with the same names.
Atom Orbitallerinin Simetrileri-1 • When bonds are formed, atomic orbitals combine according to their symmetry. • Symmetry properties and degeneracy of orbitals can be learned from corresponding character tables by their inspection. Hold in mind the following transformational properties: Totaly symmetric
Atom Orbitallerinin İndirgenemez Gösterimleri-1 ÖRNEK: SO2 molekülünde py orbitalinin indirgenemez gösterimini oluşturunuz. S O O py has the same symmetry properties as Ty and Rx vectors
Atom Orbitallerinin İndirgenemez Gösterimleri-2 ÖRNEK: D4h nokta grubunda px ve py orbitallerinin İG oluşturunuz. y the px and py orbitals in a system with a C4 axes. C4 px px’ py py py’ px x A 2x2 transformation matrix In matrix form:
Atom Orbitallerinin İndirgenemez Gösterimleri-3 ÖRNEK: D4h nokta grubunda dx2-y2 orbitalinin indirgenemez gösterimini oluşturunuz. sh Au Au C4 [AuCl4]- sh.[d x2-y2] = (+1) .[d x2-y2] Au C4.[d x2-y2] = (-1) .[d x2-y2]
Vektörlerin İndirgenemez Gösterimleri-1 ÖRNEK: Ty vektörünün indirgenemez gösterimini oluşturunuz. Ty unit vector on each atom represents translation in the y direction z z C2 S y - y S O O O O E .(Ty) = (+1) TyC2.(Ty) = (-1) Ty syz .(Ty) = (+1) Ty sxz .(Ty) = (-1) Ty
Vektörlerin İndirgenemez Gösterimleri-2 ÖRNEK: 1-SO2 molekülünde Rz dönme vektörünün İG oluşturunuz. 2- Simetrisini belirleyiniz. x E(Rz) = (+1)(Ty) C2(Rz)= (+1)(Ty) sxz(Rz) = (-1)(Ty) syz(Rz) = (-1)(Ty) y A2 simetrisi
Vektörlerin İndirgenemez Gösterimleri-3 sv -Rz E +Rz C2 +Rz sd -Rz C4 +Rz ÖRNEK: Rz dönme vektörünün indirgenemez gösterimini oluşturunuz. A2 transforms like a rotation around z.
İndirgenebilir GösterimlerReducible representations • Bir grubunGrindirgenebilir gösterimi,Gi indirgenemez gösterimlerin toplamından meydana gelmiştir. • nisayısı, i indirgenemez gösteriminin, indirgenebilir gösterimde kaç tane bulunduğunu gösterir. n İndirgenebilir Gösterim
İndirgeme Formülü ni = indirgenemez gösterim sayısı h = nokta grubunun simetri işlemi sayısı (grup derecesi) c(R) = indirgenebilir temsildeki R işleminin karakteri ci(R) = i indirgenemez temsildeki R işleminin karakteri Best to get used to this by practice!
İndirgeme İşlemi-1 ÖRNEK: Aşağıdaki rindirgenebilir temsili, indirgenemez gösterimlerine indirgeyiniz. Gr=2A1+E
İndirgeme İşlemi-2 red=2A1+ B1 + B2
İndirgeme İşlemi-3 s(xz) s(yz) C2v E C2 G3N +9 -1 +1 3 aA1 = (1/4)[ ( 1x9x1) + (1x-1x1) + (1x1x1) + (1x3x1)] = (12/4) =3 aA2 = (1/4)[ ( 1x9x1) + (1x-1x1) + (1x1x-1) + (1x3x-1)] = (4/4) =1 aB1 = (1/4)[ ( 1x9x1) + (1x-1x-1) + (1x1x1) + (1x3x-1)] = (8/4) =2 aB2 = (1/4)[ ( 1x9x1) + (1x-1x-1) + (1x1x-1) + (1x3x1)] = (12/4) =3 G3N = 3A1 + A2 + 2B1 + 3B2
İndirgeme İşlemi-4 E 2C3 3sv C3v 15 0 3 G3N n(A1) = 1/6[(1x 15x1) + (2 x 0 x 1) + (3 x 3x 1)] = 1/6 [15 + 0+ 9] = 4 n(A2) = 1/6[(1 x 15 x 1) + ( 2 x 0 x 1) + (3 x 3x –1)] = 1/6 [15 + 0 -9] = 1 n(E) = 1/6[ (1 x 15 x 2) + (2 x 0 x –1) + (3 x 3 x 0)] = 1/6[30 + 0 + 0 ] =5 G = 4A1 + A2 + 5E
IR Seçim Kuralı IR seçim kuralına göre, bir titreşim esnasında dipol değişimi oluyorsaelektromanyetik dalga ile etkileşebilir. Titreşim modu, o nokta grubuna ait öteleme vektörlerinden (Tx,Ty, Tz) en az biri ile aynı simetride ise, bu IR geçişi simetri izinlidir. Nokta Grubu IR aktif titreşim modları A1, B1, B2 E', A2' ' A2u, Eu T2 T1u C2v D3h D4h Td Oh