§4.1 几个有用的排列组合函数

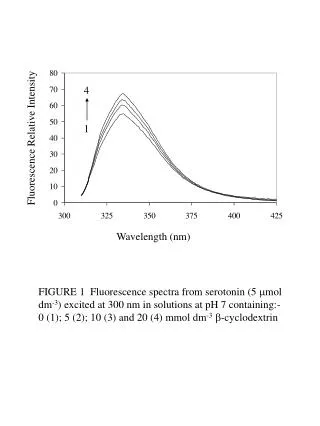
Chapter 4概率统计中的Matlab • §4.1几个有用的排列组合函数 • 一、基本公式如：>> nchoosek(5,3)，nchoosek(20,6) ans= 10 ans = 38760

如：>> factorial(6),factorial(10) ans= 720 ans = 3628800

如：>> perms([1 3 5]) ans = 5 3 1 5 1 3 3 5 1 3 1 5 1 3 5 1 5 3

如：>> combnk([2 3 6 7 8],3) ans = 6 7 8 3 7 8 3 6 8 3 6 7 2 7 8 2 6 8 2 6 7 2 3 8 2 3 7 2 3 6

如：>> randperm(5) ans = 3 4 5 2 1

二、产生随机数的两种方法 • rand(1,n)产生1行n列，即 • n个（0，1）之间的随机数如： >> rand(1,8) ans = 0.2760 0.6797 0.6551 0.1626 0.1190 0.4984 0.9597 0.3404

注：(1)由此可产生任意区间(a,b)的随机数，即 • Rand(1,n)*（b-a）+a >> rand(1,8)*3+2 ans = 2.2276 2.1619 3.5924 4.3375 4.8020 2.3897 3.7065 3.4082 如：此即是产生了区间（2，5）之间的8个随机数。

ceil: 往上取整，即若0.12取为1； • fix：靠近零取整，即若0.12取为0，如： >> A1=rand(1,8)*3+2 A1 = 2.7889 3.9622 4.0676 4.2445 3.3516 2.2515 2.6869 4.7400

>> ceil(A1) ans = 3 4 5 5 4 3 3 5 >> fix(A1) ans = 2 3 4 4 3 2 2 4

2. unidrnd(n,1,m)：产生最大值为n的 1行m列(m个)的随机自然数。 >> unidrnd(9,1,5) ans = 8 9 2 9 6 如： >> unidrnd(9,1,5) ans = 1 3 5 9 9

三、随机试验的计算机模拟 • 例、《概统》书上习题一的13题 • 设有6个相同的球以等可能地落入10个盒子中的每一个，其中盒子是可辨的并且盒子能容纳的球数不限。求 • （1）某一个指定的盒子中恰有2个球的概率； • （2）某指定的4 个盒子中正好有3个球的概率。

function P = fun1_13(N) % P返回实验成功的概率 % N表示随机模拟进行的次数 n=0; % n表示实验成功的次数 fork=1:N y=zeros(1,10);%初始化10个盒子 fori=1:6 %进行6次扔球实验

r=unidrnd(10); %产生1到10之间的随机正整数，表示球掉入的盒子号 y(r)=y(r)+1; %该盒子内的球数加1 end if y(1)==2 %某个指定的盒子，不妨假设为第一个盒子 n=n+1; end end P=n/N;

>> fun1_13(10) ans = 0 >> fun1_13(20) ans = 0.0500 >> fun1_13(30) ans = 0.0333

>> fun1_13(1000) ans = 0.0880 >> fun1_13(1000) ans = 0.0960 >> fun1_13(10000) ans = 0.1005

>> fun1_13(1e4) ans = 0.0949 >> fun1_13(1e5) ans = 0.0980 >> fun1_13(1e5) ans = 0.0985 >> fun1_13(1e5) ans= 0.0983

例、《概统》书上习题一的31题 • 乒乓球有白色与黄色两种颜色，一口袋内有两个乒乓球，但不知道口袋内两个乒乓球的颜色。 • 现在从口袋中任取一个乒乓球，发现是黄色的，然后返回口袋充分混合，求从口袋中再取出一个黄色乒乓球的概率。

function P = fun1_31(N) % P返回实验成功的概率 % N表示随机模拟进行的次数 n=0;%n表示实验成功的次数 m=0;%m表示有效实验次数（第一次取到白色的为无效实验） for k=1:N y=unidrnd(2,1,2);%产生1行2列两个不大于2的随机正整数，1代表黄色，2代表白色

if y(1)==2 %白色,不符合实验要求， 从新开始实验 continue; end m=m+1; r=unidrnd(2); %产生不大于2的数，表示随机取第一个或第二个球 if y(r)==1 n=n+1; end end P=n/m;

>> fun1_31(1e5) ans = 0.7489 >> fun1_31(1e5) ans = 0.7517

>> fun1_31(1e5) ans = 0.7551 >> fun1_31(1e6) ans = 0.7504

作业 • 1、利用Matlab验证，对任意的正整数m,n及非负整数k,下式成立，并由此写出二项分布的可加性质。

1、设每个人的生日在一年的365天中的任意一天是等可能的.1、设每个人的生日在一年的365天中的任意一天是等可能的. • (1)给出在一个 • 至少有两个人的生日相同的概率P2(n)的计算公式。 • (2)试用Matlab软件分别算出P2(k),k=2,3, • ……,100

(3)利用产生随机数的方法，随机产生 • 30个1到365之间的正整数，用计算机 • 模拟30个人中至少有两个人生日相同 • 的概率，模拟5次，并与(2)的结果进行 • 对照，与你自己的想象有没有不同，写出你的想象。

§4.1 几个有用的排列组合函数