1 / 35

Lagrangian Models

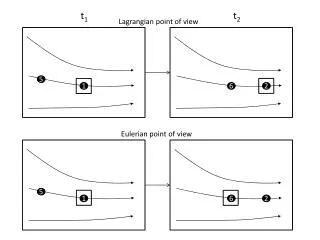
Lagrangian Models. Anne Douglass Code 613.3 Atmospheric Chemistry and Dynamics Branch NASA Goddard Space Flight Center . Type 1 Requires specific knowledge of air parcel origin Solar history Temperature history Valid for 5-7 days (some cases a few days longer) . Type 2

sidone
Download Presentation

Lagrangian Models

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Lagrangian Models Anne Douglass Code 613.3 Atmospheric Chemistry and Dynamics Branch NASA Goddard Space Flight Center

  2. Type 1 Requires specific knowledge of air parcel origin Solar history Temperature history Valid for 5-7 days (some cases a few days longer) Type 2 Study “overall transport properties” Strat/trop exchange Tropical isolation Requires large numbers of parcels and statistical analysis of their behavior Lagrangian Models Web of Science Search 1994 - present Journal of Geophysical Research Atmospheres Geophysical Research Letters “trajectory” - title, key word, abstract - ~500 publications Two main types of applications

  3. Assumptions about Trajectory Transport • Parcels have no inertia (m = 0), D = “Drag”,Vw = wind • Parcels have no size yet “represent” their surroundings • Parcels don’t know about each other except when some kind of explicit mixing is included

  4. Trajectory Model Formulations • Kinematic Trajectory Models - use “w” field from 3D GCM or assimilation • Advantages • Consistent with CTM model transport • Can resolve mesoscale convective motions and cloud transport if 3D model can. • Disadvantages • Inadequate time resolution of adiabatic motion can lead to enhanced diabatic drift • Isentropic/Diabatic Trajectory Models • Advantages • Conservation of entropy - adiabatic motions removed • Diabatic motion usually more accurate than vertical motion field since motion dependent on T not “w” • Disadvantages • What is the best way to treat surface interaction, convection and moist processes?

  5. Errors There are different approaches to solving the trajectory equation: • The “constant acceleration” solution • Neglects higher order terms in the Taylor series expansion of the first equation (source of truncation errors). • OTHER things to think about • time resolution of wind fields • interpolation errors • vertical wind issues • wind field errors • tropospheric process errors Stohl A., Computation, Accuracy and Applications of Trajectories - A Review and Bibliography, Atmospheric Environment, 32, 947-966, 1998.

  6. Types of applications: • interpretation of aircraft and satellite constituent observations • trajectory mapping for satellite validation • Morris et al., Trajectory mapping: A tool for validation of trace gas observations, J. Geophys. Res., 105, 17,875-17,894, 2000. • Danilin, M. Y., Comparison of ER-2 aircraft and POAM III, MLS, and SAGE II satellite measurements during SOLVE using traditional correlative analysis and “trajectory hunting technique”, J. Geophys. Res., 107, doi:10.1029/2001JD000781, 2002. • overall transport properties

  7. Interpretation of stratospheric constituent observations Assume you can come up with a solution to initialization issues for constituents that change on time scales of the integration e.g., NOx/Noy Use the trajectories to account for solar history photolysis rates overhead O3 column clouds reflectivity Keep some sense of how errors related to mixing or position errors in the trajectories can impact results.

  8. APPLICATION 1 - Use back trajectories + photochemical model to interpret stratospheric aircraft observations NASA’s ER-2 was deployed for the Photochemistry of Ozone Loss in the Arctic Region in Summer (POLARIS) mission flown during the summer of 1997 to measure radicals responsible for the summer photochemical destruction of ozone. One key aspect of this decline is the concentration of nitrogen radicals, and their abundance relative to the reservoir HNO3. Pierson, J. M. et al., Influence of air mass histories on radical species during the Photochemistry of Ozone Loss in the Arctic Region in Summer (POLARIS) mission, J. Geophys. Res., 105, 15,185-15,199, 2000.

  9. 10-Day Back Trajectories for 970426 Parcel Theta (K) 0 349.0 6 493.0 10 502.0 14 502.0 18 507.0 22 504.0 26 500.0 30 481.0 30 26 22 14 0 26 High latitude summer is nearly continuously in sunlight, but back trajectories show that late April air parcels intercepted by the ER-2 have different solar history.

  10. There are chemical differences (apparent in both plots). The outliers (from the late April flight shown on the previous slide) join the main group when the solar history is accounted for using back trajectories. Subsequent laboratory measurements of the rates for NO2 + OH + M  HNO3 + M and OH + HNO3 NO3 + H2O greatly reduce the model - measurement disparity. NOx/Noy modeled NOx/Noy measured NOx/Noy modeled NOx/Noy measured April 26 points are outliers

  11. Issues Initialization NOx/NOy was initialized in for both calculations using observations at the flight track. The steady state calculation produces higher NOx/NOy because periods of darkness and latitudinal variation of solar zenith angle are not accounted for. Mixing This calculation assumes no mixing. Trajectory errors Although 10 days is a long time for a backward trajectory, the solar history is likely to have smaller errors than the exact location, and this is the main source of error for the steady-state comparison. (and trajectories are more serene in a summer circulation . . .)

  12. APPLICATION 2 - REVERSE DOMAIN FILL If you start forward trajectories from a regular grid (no matter how dense), the result (no matter how long the calculations) is an irregular distribution of endpoints. If you start from a regular grid and go backwards, the endpoints are similarly irregular. The application called Reverse Domain Fill (RDF) starts backward trajectories from a dense regular grid, and produces a distribution of endpoints. Take observations that you have and interpolate to this distribution.

  13. Reverse Domain Filling (RDF) Regular grid Time T • Step 1 • Run a back trajectories starting with a regular gridded array • Step 2 • Interpolate observations to back trajectory points • Step 3 • Copy values forward to regular grid Time T-DT

  14. RDF Calculations Adiabatic Wave breaking features are better resolved PV is higher Smoothed RDF not the same as analyzed PV Diabatic 5o box car smoothed

  15. N2O 1150 K Jan 11, 1992 Gridded ISAMS RDF from Jan 10 RDF from Jan 9 RDFs for Jan 11 are calculated using back trajectories from an equal area grid. Back trajectories are 1 to 7 days duration. Each day’s data from the terminus of the back trajectory is projected to the equal area grid. Filamentary structures appear as the back trajectory duration lengthens. Sutton et al., High Resolution Stratospheric Tracer Fields Estimated from Satellite Observations Using Lagrangian Trajectory Calculations, JAS 1994. RDF from Jan 5 RDF from Jan 4

  16. The left panel RDF for January 7 projects gridded ISAMS data from January 2. The center panel RDF for the same day) projects the along-track data from January 2. The right hand panel is the along-track data (Jan. 2). The main features are the same in (a) and (b) (disregarding the missing data), showing that the winds play the predominant role in producing the RDF structure, not fine structure from the along-track observations.

  17. In January/February this year a DC-8 mission took place out of Pease New Hampshire (Polar Aura Validation Experiment PAVE). One of the instruments on the DC-8 is an ozone lidar AROTEL. The DC-8 flight track nearly coincided with the Aura track for the Microwave Limb Sounder. The GSFC Chemistry and Transport Model used winds and temperatures from Goddard’s Global Modeling and Assimilation Office meteorological fields to simulate ozone (and other constituents). GMAO assimilated fields are 1 lat x 1.25 long horizontal resolution. The CTM is usually run at 2 lat x 2.5 long to meet computing constraints.

  18. 1x1.25 MLS (upper left) and AROTAL (lower left) show a sharp vortex edge. CTM edges are sharper at 1x1.25 (upper right) than at 2x2.5 (lower right), but not nearly as sharp as observed. 2 x 2.5

  19. 1x1.25 A few days later, MLS and AROTAL show a structure (a filament) that is also apparent in the 1x1.25 CTM but only vaguely hinted at in the 2x2.5 CTM. At 2 x 2.5 the grid point model “overmixes”. Does this matter to O3 evolution (or to a global predictive model?) 2 x 2.5

  20. 2 Days 6 Days 15 Days 10 Days

  21. The RDFs show that the GMAO winds contain the information to produce a filament that looks like the observed filament. At the same time, the RDFs show more and more structure as the “mixing free” calculation goes back farther and farther in time. This gives a sense of the importance of mixing processes in the stratosphere - there is *too much* structure in the RDF for the longest back trajectories. How, when, where do parcels mix? Can models simulate mixing on appropriate temporal and spatial scales?

  22. Lagrangian Mixing Algorithms • RDF’s can produce infinitely fine structure - such fine structure is not observed => must mix parcels at some point • Mixing algorithm types • Proximity algorithms • Parcels which move within a certain distance mix with neighbors • Conditional Algorithms • Nearby parcels mix under certain flow conditions (most useful when small number of parcels used)

  23. Proximity Algorithm D=R2/Dt D = diffusion coefficient Parcels Mix Dt Radius of interaction R

  24. The CLaMS model was constructed to take advantage of the high spatial resolution afforded by the RDF approach, and at the same time to simulate mixing processes that also play a role in constituent distributions. • The CLaMS mixing scheme has the following properties • ability to represent the scale collapse associated with a 2D turbulent flow • mixing rates depend on the flow pattern and are smallest where the deformation rate is smallest (and vice versa) McKenna et al., A new Chemical Lagrangian Model of the Stratosphere (CLaMS) 1. Formulation of advection and mixing, J. Geophys. Res., 107, 2002.

  25. Start with a uniform grid - think of a grid point as enclosed by a circle After some time the circle is distorted into an ellipse. t=t0 t=t0+t The Lyapunov exponent is the mean logarithmic expansion rate of the principal axes The Lyapunov exponent varies (e.g., small at transport barriers, larger in the surf zone). The CLaMS algorithm “mixes” when the Lyapunov exponent exceeds a critical value.

  26. N2O 700 K November 10 t = 12 hours “low resolution” r0 ≈ 200 km (7000 grid points) “pure” advection (no mixing) c = ∞ Moderate mixing c = 1.2 days-1 Excessive mixing c = 0.6 days-1 N2O (ppbv) 220 200 180 160 140 120 100 80 60 40 20 0

  27. CH4 at 475 K on April 8 after 44 days simulation. CLaMS low resolution simulation (r0 ≈ 200 km) CLaMS high resolution simulation r0 ≈ 60 km Isentropic advection using Prather’s numerical transport scheme CH4 (ppmv) 1.59 1.51 1.43 1.35 1.27 1.19 1.11 1.03 0.95

  28. CLaMS produces structure in this simulation of ozone change for winter 1999/2000 at 450K. Ozone loss is sensitive to chlorine deactivation (ClO + NO2 + M  ClONO2 + M) and denitrification, both of which are sensitive to excess mixing.

  29. Winds contain the information to produce filaments In some cases, maintaining the separation of air masses and structure is important to the photochemical processes. Importance of this sort of structure to the global scale is less clear and a present topic of investigation.

  30. Massive numbers of trajectories give insight into the overall transport properties of meteorological fields (whether from a data assimilation system or a general circulation model). • Schoeberl et al. used diabatic and kinematic trajectories to compare tropical transport produced by UKMO and GEOS data assimilation systems. • Diabatic trajectories • parcels transported along isentropic surfaces by the large-scale wind field • parcels moved across isentropic surfaces by the net diabatic heating • Kinematic trajectories • parcels transorted horizontally on pressure surfaces • parcels moved vertically by the omega field (dp/dt, where p is the pressure) • Schoeberl et al., A comparison of the lower stratospheric age spectra derived from a general circulation • model and two data assimilation system, J. Geophys. Res., 108, 2003

  31. These trajectory calculations clearly show the problems with the meteorological data sets. Both diabatic and kinematic trajectories for UKMO and FVDAS show that the air in the central tropics comes from middle latitude - this level of horizontal mixing is not support by aircraft or satellite observations. It is important that using the heating rates to specify the vertical transport does not solve the problem. Although either of these simulations will behave more physically at polar latitudes when the vertical transport is specified by the heating rates, there are issues with mixing and mass balance that affect the simulations and affect comparisons of simulated and observed constituent fields.

  32. Summary The trajectory approach is an important tool in process study land. Trajectories • can provide insight into photochemical processes through application to interpretation of measurements • can provide insight into transport and mixing processes • can reveal large scale characteristics of atmospheric flow The trajectory approach has some issues/limitations: • position errors • mixing issues • tropospheric processes (convection, clouds, boundary layer) The trajectory approach will serve the user best if s/he understands the limitations and avoids the pitfalls of the “black box”.

More Related