The Ferry Cover Problem
1.35k likes | 1.57k Views
The Ferry Cover Problem. Michael Lampis - Valia Mitsou National Technical University of Athens. Wolf. Goat. Cabbage. Guard. Boat. Previous Work. “Propositiones ad acuendos iuvenes”, Alcuin of York, 8th century A.D (in latin). We propose a generalization of Alcuin’s puzzle.

The Ferry Cover Problem
E N D
Presentation Transcript
The Ferry Cover Problem Michael Lampis - Valia Mitsou National Technical University of Athens
Previous Work • “Propositiones ad acuendos iuvenes”, Alcuin of York, 8th century A.D (in latin). • We propose a generalization of Alcuin’s puzzle
Our generalization • We seek to transport n items, given their incompatibility graph. • Objective: Minimize the size of the boat • We call this the Ferry Cover Problem
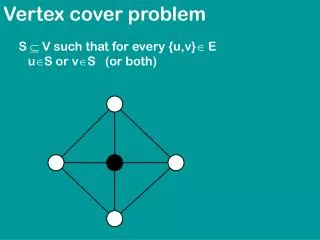
The Ferry Cover Problem Lemma: OPTVC (G) ≤ OPTFC (G) ≤ OPTVC (G) + 1 Graphs are divided into two categories: • Type-0, ifOPTFC (G) = OPTVC (G) • Type-1, if OPTFC (G) = OPTVC (G) + 1
Hardness and Approximation Results • Ferry Cover is NP and APX-hard (like Vertex Cover [Håstad1997]). • A ρ-approximation algorithm for Vertex Cover yields a (ρ+1/ OPTFC)-approximation algorithm for Ferry Cover.