1 / 10

Area Calculations for Kite and Rhombus in Coordinate Plane

This guide covers the methods for finding areas of a kite and a rhombus using their diagonal lengths. For a kite, the area formula ( A = frac{d_1 times d_2}{2} ) applies, with one diagonal being four times the length of the other. The example demonstrates how to solve for the diagonal lengths with given area conditions. The second section focuses on calculating the area of a rhombus using the lengths of its diagonals derived from vertex coordinates in a coordinate plane.

senona
Download Presentation

Area Calculations for Kite and Rhombus in Coordinate Plane

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

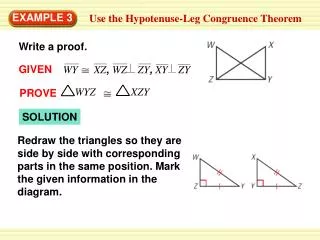
  1. Standardized Test Practice EXAMPLE 3 SOLUTION Draw and label a diagram. Let xbe the length of one diagonal. The other diagonal is twice as long, so label it 2x. Use the formula for the area of a kite to find the value of x.

  2. 1 A = d1d2 2 1 72.25 = (x)(2x) 2 Standardized Test Practice EXAMPLE 3 Formula for area of a kite Substitute72.25for A, xfor d1, and2xford2.

  3. ANSWER The correct answer is C. Standardized Test Practice EXAMPLE 3 72.25 = x2 Simplify. 8.5 = x Find the positive square root of each side. The lengths of the diagonals are8.5 inches and 2(8.5) = 17 inches.

  4. You have a map of a city park. Each grid square represents a 10 meter by 10 meter square. Find the area of the park. Find an area in the coordinate plane EXAMPLE 4 City Planning

  5. b1 = BC = 70 – 30 b2 = AD = 80 – 10 h = BE = 60 – 10 Find an area in the coordinate plane EXAMPLE 4 SOLUTION STEP 1 Find the lengths of the bases and the height of trapezoid ABCD. = 40 m = 70 m = 50 m

  6. 1 1 A = h(b1 + b2) = (50)(40 + 70) 2 2 ANSWER The area of the park is 2750square meters. Find an area in the coordinate plane EXAMPLE 4 STEP 2 Find the area of ABCD. = 2750

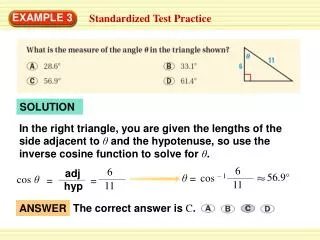
  7. Draw and label a diagram. Let xbe the length of one diagonal. The other diagonal is 4 times as long, so label it 4x. Use the formula for the area of a kite to find the value of x. 4x x for Examples 3 and 4 GUIDED PRACTICE 4. The area of a kite is 80square feet. One diagonal is 4 times as long as the other. Find the diagonal lengths. SOLUTION

  8. 1 A = d1d2 2 1 80 = (x(4x)) 2 2√ 10 = x The lengths of the diagonals ared1 = 2 √10 ft d2= 4(2 √ 10 ) = 8 √10 ft. ANSWER for Examples 3 and 4 GUIDED PRACTICE Formula for area of a kite Substitute so forA, xfor d1, and4xford2. 80 = 2 x2 Simplify. Find the positive square root of each other.

  9. for Examples 3 and 4 GUIDED PRACTICE 5. Find the area of a rhombus with vertices M(1, 3), N(5, 5), P(9, 3), andQ(5, 1). SOLUTION N P M Q STEP 1 Find the lengths of the diagonals (MP, NQ) of the rhombus MNPQ.

  10. d1 = NP d2 = NQ = 9– 1 = 5 –1 1 1 A = b1 b2 = 8 4 2 2 ANSWER The area of the rhombus MNPQ is 16units2. for Examples 3 and 4 GUIDED PRACTICE = 8 = 4 Find the area of MNPQ. STEP 2 = 16 units2.

More Related