1 / 13

Understanding Isosceles Triangle Theorems and Properties

This resource explores the fundamental properties of isosceles triangles, focusing on key theorems such as the Isosceles Triangle Theorem, which states that if two sides are congruent, the angles opposite those sides are also congruent. It elaborates on related concepts such as the importance of angle bisectors and congruency in triangles. The text also addresses equilateral triangles and their unique properties, including connections between angle measures and side lengths. Practice problems are included to reinforce understanding of these concepts.

sal
Download Presentation

Understanding Isosceles Triangle Theorems and Properties

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. 4.6 The Isosceles Triangle Theorems Base Angles and Opposite Sides Hypotenuse - Leg

  2. Parts of an Isosceles Triangle

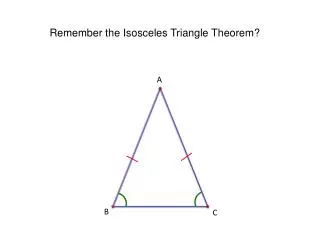
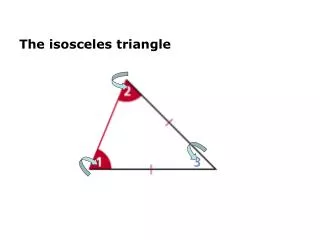
  3. Isosceles Triangle Theorem If two sides of a triangle are congruent, then the angles opposite those sides are congruent.

  4. Isosceles Triangle Theorem If two sides of a triangle are congruent, then the angles opposite those sides are congruent. Given: Bisect angle A So by SAS So By C.P.C.T.

  5. Corollary of Isosceles Triangle Theorem An equilateral triangle is also equiangular An equilateral triangle has three 60 degree angles. The bisector of the vertex angle of an isosceles triangle is perpendicular to the base at its midpoint.

  6. Another Theorem If two angles of a triangle are congruent, then the sides opposite those angles are congruent. What is this compared to the Isosceles Triangle Theorem? An equiangular triangle is also equilateral.

  7. Solve for x and y

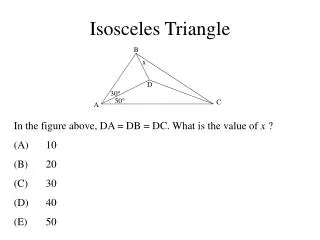
  8. Solve for angles… 2,3,4 Given:

  9. Hypotenuse – Leg (HL) In two right triangles if the hypotenuse and one leg are congruent, then the triangles are congruent. To use this you must show Right Triangles

  10. Solve for v

  11. Find the missing side

  12. Homework Page 239 – 242 # 9 – 25 odd, 34 -37, 39

  13. Homework Page 239 – 242 # 8 -24 even 29- 33

More Related