1 / 8

トーナメント戦における強弱関係

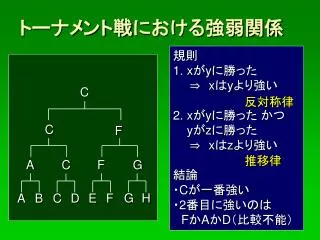
トーナメント戦における強弱関係. 規則 1. x が y に勝った 　　⇒　 x は y より強い 2. x が y に勝った かつ y が z に勝った 　　⇒　 x は z より強い 結論 ・ C が一番強い ・ 2 番目に強いのは F か A か D （比較不能）. C. 反対称律. C. F. 推移律. F. A. C. G. A. B. E. F. G. C. H. D. 反対称律. 対偶. 関係グラフにおいて 相異なる要素間には高々一方向にしか辺がない. 関係グラフとハッセ図. a.

quinn-beach
Download Presentation

トーナメント戦における強弱関係

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. トーナメント戦における強弱関係 規則 1. xがyに勝った 　　⇒　xはyより強い 2. xがyに勝った かつ yがzに勝った 　　⇒　xはzより強い 結論 ・Cが一番強い ・2番目に強いのは FかAかD（比較不能） C 反対称律 C F 推移律 F A C G A B E F G C H D

  2. 反対称律 対偶 関係グラフにおいて 相異なる要素間には高々一方向にしか辺がない

  3. 関係グラフとハッセ図 a ・反射的関係のループを除く f b ・推移的に得られる関係の 有向辺を除く xRz zRy なる　 z があれば xRyの有向辺を除く e c d ・上位の要素を上に配置し 辺の向きをなくす 関係グラフ

  4. 関係グラフとハッセ図 a ・反射的関係のループを除く f b ・推移的に得られる関係の 有向辺を除く xRz zRy なる　 z があれば xRyの有向辺を除く e c d ・上位の要素を上に配置し 辺の向きをなくす 関係グラフ

  5. 約数関係 12 8 6 2 3 1

  6. 集合の包含関係 {a,b,c} {a,b} {b,c} {a,c} {a} {b} {c} φ

  7. 上限と下限 順序集合(X;≦) において • 極大元： 自分より大きい（上位の）要素を持たない元　 有限集合中に1個以上存在 • 最大元： 唯一の極大元（もしあれば） max(X) 極小元、最小元( min（X) )も同様に定義する 順序集合(X; ≦)と、その部分集合Aにおいて • Aの上界 Upper(A)={x | x∈X, すべてのa∈Aに対しa≦x} • Aの上限 sup(A)=min(Upper(A)) 下界、下限( inf(A) )も同様に定義する

  8. Aの最小上界 （上限） Aの下限 Aの上界 例 極大元 最大元 a c b A e d h g f Aの下界 極小元 最小元なし

More Related