1 / 9

Projections of Multivariate Data onto Vectors

This article explores the concept of projecting multivariate data onto vectors using a data matrix ( X' ) and a vector ( a ). We define ( Y' = X'a ) and discuss how the values in ( Y' ) represent the coordinates of each observation along the vector ( a ). Through illustrative examples, we compute projections for given observations ( x_1, x_2, x_3 ) and demonstrate how to derive their projections onto the specified vector ( a ), enhancing understanding of data representation in multivariate analysis.

owen
Download Presentation

Projections of Multivariate Data onto Vectors

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

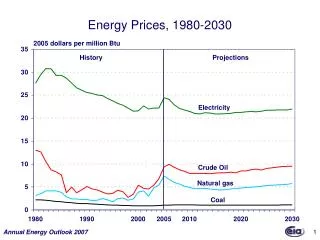
  1. Aside: projections onto vectors • If X is an np data matrix and a a p1 vector then Y= Xais the projection of X onto a • Values of Y give the coordinates of each observation along the vector a • Example: x1=(1, 2), x2=(2, 1), x3=(1,1) a=(3, 4)/5, • So Multivariate Data Analysis

  2. Aside: projections onto vectors x1 2  x3 x2   (0,0)  1 Multivariate Data Analysis

  3. Aside: projections onto vectors x1 2  x3 x2   (0,0)  1 a=(3,  4)/5 Multivariate Data Analysis

  4. Aside: projections onto vectors x1 2  x3 x2   y1 (0,0)  1 a=(3,  4)/5 Multivariate Data Analysis

  5. Aside: projections onto vectors x1=(1, 2) 2  x3 x2   y1 = (3142)/5 = 1 (0,0)  1 a=(3,  4)/5 Multivariate Data Analysis

  6. Aside: projections onto vectors x1 2  x3 x2   y1 = 1 (0,0)  1 y2 = 2/5 a=(3,  4)/5 Multivariate Data Analysis

  7. Aside: projections onto vectors x1 2  y3 = 7/5 x3 x2   y1 = 1 (0,0)  1 y2 = 2/5 a=(3,  4)/5 Multivariate Data Analysis

  8. Aside: projections onto vectors 2 y3 = 7/5   y1 = 1 (0,0)   1 y2 = 2/5 a=(3,  4)/5 Multivariate Data Analysis

  9. Aside: projections onto vectors 2      (0,0)   1 a=(3,  4)/5 Multivariate Data Analysis

More Related