1 / 23

Electric Potential

Electric Potential. CONSERVATIVE FORCES. A conservative force “gives back” work that has been done against it. Gravitational and electrostatic forces are conservative Friction is NOT a conservative force. CONSERVATIVE FORCES.

omar-carr
Download Presentation

Electric Potential

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Electric Potential

  2. CONSERVATIVE FORCES A conservative force “gives back” work that has been done against it Gravitational and electrostatic forces are conservative Friction is NOT a conservative force

  3. CONSERVATIVE FORCES A conservative force “gives back” work that has been done against it When we lift a mass m from ground to a height h, the potential energy of the mass increases by mgh. If we release the mass, it falls, picking up kinetic energy (or speed). As the mass falls, the potential energy is being converted into kinetic energy. By the time it reaches the ground, the mass has acquired a kinetic energy ½ mv2 = mgh, and it’s potential energy is zero. The gravitational force ‘gave back’ the work that we did when we lifted the mass.

  4. CONSERVATIVE FORCES A conservative force “gives back” work that has been done against it The gravitational force is a conservative force. The electric force is a conservative force as well. We will be able to define a potential energy associated with the electric force. A charge will have potential energy when in an electric field. Work done on the charge (by an external agent, or by the field) will result in changes in the potential energy of the charge.

  5. CONSERVATIVE FORCES When the total work done by a force F, moving an object over a closed loop, is zero, then the force is conservative  F is conservative The circle on the integral sign indicates that the integral is taken over a closed path The work done by a conservative force, in moving and object between two points A and B, is independent of the path taken is a function of A and B only is NOT a function of the path selected A conservative force “gives back” work that has been done against it

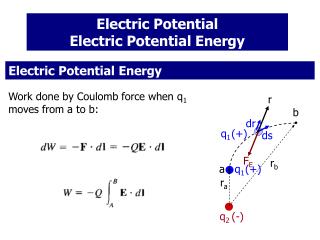
  6. The change UAB in potential energy, associated with a conservative force, is the negative of the work done by that force, as it acts from point A to point B UAB = -WAB UAB = UB – UA = potential energy difference between A and B POTENTIAL ENERGY

  7. The change UAB in potential energy, associated with a conservative force F, is the negative of the work done by that force, as it acts (over any path) from point A to point B UAB = -WAB = -  F.dr UAB = UB – UA = potential energy difference between A and B B A POTENTIAL ENERGY Potential energy is a relative quantity, that means, it is always the difference between two values, or it is measured with respect to a reference point (usually infinity). We will always refer to, or imply, the change in potential energy (potential energy difference) between two points.

  8. E L A B • • UAB =q E L POTENTIAL ENERGY IN A CONSTANT FIELD E The potential energy difference between A and B equals the negative of the work done by the field as the charge q is moved from A to B UAB = UB – UA = -WAB = -FE L = q E L

  9. L A B • • dL UB - UA =q E L UAB =q E L POTENTIAL ENERGY IN A CONSTANT FIELD E E Potential energy difference between A and B UAB = UB – UA = -  q E.dl But E = constant, and E.dl = -1 E dl, then: UAB = -  q E.dl =  q E dl = q E  dl = q E L

  10. UAB = UB – UA = - FE L B A POTENTIAL ENERGY IN A CONSTANT FIELD E The potential energy difference between A and B equals the negative of the work done by the field as the charge q is moved from A to B UAB = q E L when the +q charge is moved against the field

  11. E L A B • • • At which point (A or B) is the potential energy larger, • For a positive charge +q ? • For a negative charge –q ?

  12. L B A • • x D An electric field E = a/x2 points towards +x. Calculate the potential energy difference UAB = UB – UA for a charge +q

  13. VAB = UAB / q Electric Potential = Potential Energy per Unit Charge ELECTRIC POTENTIAL DIFFERENCE The potential energy U depends on the charge being moved. In order to remove this dependence, we introduce the concept of electric potential V VAB = VB – VA Electric potential difference between the points A and B

  14. B VAB = UAB / q = - (1/q)  q E . dL = -  E . dL A ELECTRICAL POTENTIAL DIFFERENCE The potential energy U depends on the charge being moved. In order to remove this dependence, we introduce the concept of electrical potential V VAB = UAB / q Electrical Potential = Potential Energy per Unit Charge VAB = Electrical potential difference between the points A and B

  15. E L A B • • VAB = E L ELECTRIC POTENTIAL IN A CONSTANT FIELD E The electric potential difference between A and B equals the negative of the work per unit charge, done by the field, as the charge q is moved from A to B VAB = VB – VA = -WAB /q = qE L/q = E L

  16. E L A B • • dL VAB = E L ELECTRICAL POTENTIAL IN A CONSTANT FIELD E VAB = UAB / q The electrical potential difference between A and B equals the work per unit charge necessary, for an external agent, to move a charge +q from A to B VAB = VB – VA = -WAB /q = -  E.dl But E = constant, and E.dl = -1 E dl, then: VAB = -  E.dl =  E dl = E  dl = E L UAB =q E L

  17. E L A B • • UAB = UB – UA = -WAB = -FE L VAB = VB – VA = -WAB /q = E L VAB = E L UAB =q E L POTENTIAL ENERGY IN A CONSTANT FIELD E UAB ELECTRIC POTENTIAL IN A CONSTANT FIELD E VAB VAB = UAB / q

  18. UNITS Potential Energy U: [Joule]  [N m] (energy = work = force xdistance) Electric Potential V: [Joule/Coulomb]  [Volt] (potential = energy/charge) Electric Field E: [N/C]  [V/m] (electric field = force/charge = potential/distance)

  19. B VAB = -  E.dl A Cases in Which the Electric Field E is not Aligned with dL E A •  • B Since F = q E is conservative, the field E is conservative. Then, the electrical potential difference does not depend on the integration path. One possibility is to integrate along the straight line AB. This is convenient in this case because the field E is constant, and the angle  between E and dL is constant. B E . dl = E dl cos   VAB = - E cos   dl = - E L cos  A

  20. B VAB = -  E.dl A VAB = - E L cos  Cases in Which the Electric Field E is not Aligned with dL E X A C • •   L • B Another possibility is to choose a path that goes from A to C, and then from C to B VAB = VAC + VCB VAC = E X VCB = 0 (E  dL) Thus, VAB = E X but X = L cos  = - L cos 

  21. Rank the points A, B, and C in order of decreasing potential energy, for a charge +q is placed at the point.

  22. A B E E VAB = E L VAX = E X X L L Equipotential Surfaces (lines) Since the field E is constant Then, at a distance X from plate A All the points along the dashed line, at X, are at the same potential. The dashed line is an equipotential line

  23. E L Equipotential Surfaces (lines) X It takes no work to move a charge at right angles to an electric field E dL   E•dL = 0  V = 0 If a surface (line) is perpendicular to the electric field, all the points in the surface (line) are at the same potential. Such surface (line) is called EQUIPOTENTIAL EQUIPOTENTIAL  ELECTRIC FIELD

More Related