1 / 117

第三章 CPU 子系统

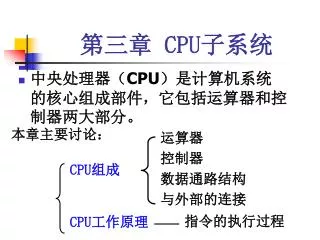
第三章 CPU 子系统. 中央处理器（ CPU ）是计算机系统的核心组成部件，它包括运算器和控制器两大部分。. 本章主要讨论：. 运算器 控制器 数据通路结构 与外部的连接. CPU 组成. CPU 工作原理. 指令的执行过程. 3.1 算术、逻辑运算基础. 计算机进行运算的特点： (1) 所有数据都是用二进制数位形式来表示的。 (2) 在机器内部，数是以编码形式即机器数来表示的。 (3) 机器运算规模有限，因而机器运算就要解决运算方法、数据表示格式及数据长度的选取、规定等问题。

neona
Download Presentation

第三章 CPU 子系统

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. 第三章 CPU子系统 • 中央处理器（CPU）是计算机系统的核心组成部件，它包括运算器和控制器两大部分。 本章主要讨论： 运算器 控制器 数据通路结构 与外部的连接 CPU组成 CPU工作原理 指令的执行过程

  2. 3.1 算术、逻辑运算基础 计算机进行运算的特点： (1)所有数据都是用二进制数位形式来表示的。 (2)在机器内部，数是以编码形式即机器数来表示的。 (3)机器运算规模有限，因而机器运算就要解决运算方法、数据表示格式及数据长度的选取、规定等问题。 (4)用计算机进行运算时，都要把复杂的运算，简化为一系列的、最基本的运算才能实现。计算机可以实现的基本运算有算术运算(加、减、乘、除等)和逻辑运算(与、或、异或等)。

  3. 3.1.1 定点加减运算 补码加减法: • 补码的一个重要特点是它可以直接进行加减法运算，并且计算简单，因此计算机中基本采用补码加减法。 • 运算规则： （1）参与运算的操作数用补码表示，符号位作为数的一部分直接参与运算，所得即为补码表示的运算结果。 （2）若操作码为加，则两数直接相加； （3）若操作码为减，则将减数变补后再与被减数相加。

  4. 3.1.1 定点加减运算 • 计算公式 [X+Y]补=[X]补+[Y]补 [X-Y]补=[X]补+[-Y]补 • 例1 已知X=9，Y=3，求[X+Y]补， [X-Y]补， [Y-X]补。 解： [X+Y]补= [X]补+[Y]补=01001+00011=01100 [X-Y]补=[X]补+[-Y]补=01001+11101=100110 [Y-X]补=[Y]补+[-X]补=00011+10111=11010

  5. 3.1.1 定点加减运算 • 例2 X=0.001010 Y=-0.100011 求[X-Y]补 解 [X]补=0.001010 [-Y]补=0.100011 则 [X-Y]补= [X]补+[-Y]补 = 0.001010 + 0.100011 = 0.101101

  6. 3.1.2 溢出判断与移位 一.溢出 机器数字长5位，其中含1位数符，补码运算，问：定点整数表示范围？ -16 ~ +15 （10000 ~ 01111） 所谓溢出就是指运算结果大于机器所能表示的最大正数或小于机器所能表示的最小负数。

  7. 3.1.2 溢出判断与移位 • 正溢：两个正数相加后结果超出允许的表示范围。 如: P100 例3-3 • 负溢：两个负数相加后结果超出允许的表示范围。 如: P100 例3-5

  8. 3.1.2 溢出判断与移位 • 溢出判别 定义：两操作数的数符分别为SA、SB，结果的数符为Sf。符号位直接参与运算，产生的符号位进位为Cf。最高有效数位产生的进位为C。 1.判别方法一： 溢出= • 只有同号数相加才能产生溢出，溢出的标志是结果数符与操作数数符相反

  9. 3.1.2 溢出判断与移位 2.判别方法二： 溢出= （Cf为符号位运算产生的进位，C为最高有效数位产生的进位。） • Cf 和C不同时表明溢出 3.判别方法三： 操作数采用双符号位（变形补码），通过运算结果的符号位进行判断：（P101) 00 —结果为正，无溢出 01—结果正溢 10 —结果负溢 11—结果为负，无溢出

  10. 3.1.2 溢出判断与移位 二. 移位 • 逻辑移位 （1） 数字代码为纯逻辑代码，没有数值意义 （2）分为：循环左移、循环右移、非循环左移、非循环右移

  11. 3.1.2 溢出判断与移位 • 算术移位 1、原码（及正数补码）移位规则：数符不变，空位补0 2、负数补码移位规则： 左移：数符不变，空位即末位补0 右移：数符不变，空位补1

  12. 3.1.2 溢出判断与移位 3. 例： • 原码和正数补码 0.0101 左移一位 0.1010 1.0101 左移一位 1.1010 00.1010 左移一位 01.0100 （*双符号位时可左移1位，第二符号位暂存数值，第一符号位仍表示符号） 1.1010 右移一位 1.0101 01.0100 右移一位 00.1010 （* 双符号位时右移1位，第二符号位暂存的数值移到最高有效位。）

  13. 3.1.2 溢出判断与移位 • 负数补码 左移： 1.1011 左移一位 1.0110 11.0110 左移一位10.1100 右移： 1.0110 右移一位 1.1011 10.1100 右移一位 11.0110

  14. 3.1.2 溢出判断与移位 三. 舍入 • 舍入的原则 使本次舍入产生的误差及累计误差都比较小 • 两种舍入规则 1、 0舍1入 2、末位“恒置1” 例： 课本P103 例3-8 ~ 例3-11

  15. 3.1.3 定点乘法运算 • 手算例子： 1101 1101 0000 1101 0.10001111 由于结果为负，所以

  16. 3.1.3 定点乘法运算 • 手算到机器实现要解决的问题 1、符号问题 解决方法：原码乘法符号单独处理，补码乘法符号参与运算 2、乘积等于各位积之和（要考虑权） “位积”是乘数的某位乘以被乘数所得到的积。 “部分积”是位积的和。 1）n位乘法运算就有n个位积，要n个寄存器来存放位积； 2）加法器难以完成n个位积的同时求和； 3）需要2n位字长的加法器，通常的加法器都是n位字长。 解决方法：n次累加与移位循环或阵列乘法器

  17. 3.1.3 定点乘法运算 • 手算的改进（将一次相加改为分步累加） 1101 01101 + 1101 100111 100111 + 0000 100111 0100111 + 1101 10001111 10001111

  18. 3.1.3.1 原码一位乘法 一. 基本思想： • 乘积的数值部分是乘数和被乘数的数值部分相乘之积。 • 乘积的符号由两数的符号异或得到（同号相乘为正，异号相乘为负）。 • 每次用一位乘数去乘被乘数，并将一位乘数所对应的位积与原部分积的累加和相加，并移位。 设 X = Sx.x1x2…xn , Y = Sy.y1y2…yn 乘积的尾数 ：P = |X| . |Y| 乘积的符号：Sp = Sx⊕ Sy

  19. 3.1.3.1 原码一位乘法 二. 举例实现 已知 X=0.1101，Y=-0.1011，求XY=？ 设置寄存器： A：存放部分积累加和、乘积高位 B：存放被乘数 C：存放乘数、乘积低位 设置初值： A = 00.0000 B = |X| = 00.1101 C = |Y| = .1011

  20. 步数 条件 操作 A C Cn B 0.1101 ×0.1011 C 1101 1101 0000 1101 0.10001111 00.0000 .1011 1） Cn=1 +B + 00.1101 00.1101 00.0110 1.101 2） Cn=1 +B + 00.1101 01.0011 00.1001 11.10 3） Cn=0 +0 + 00.0000 00.1001 00.0100 111.1 4） Cn=1 +B + 00.1101 01.0001 00.1000 1111 X原×Y原 = 1.10001111

  21. 三. 算法流程 0 A、X B、Y C、0 CR Cn = 1 ？ CR = n ？ 1/2（A+B） A，C 1/2（A+0） A，C CR + 1 CR Sx + Sy SA N Y N Y

  22. 3.1.3.1 原码一位乘法 四. 运算规则 （1）操作数、结果用原码表示； （2）绝对值运算，符号单独处理； （3）被乘数(B)、累加和(A)取双符号位； （4）乘数末位(Cn)为判断位，其状态决定 下步操作； （5）作n次循环（累加、右移）。

  23. C4 C3 C2 C1 A4 A3 A2 A1 CPA CPC 门4 门3 门2 门1 门4 门3 门2 门1 ∑4 ∑3 ∑2 ∑1 C4 C3 C2 1/2∑ A C +A +B A1 B1 3.1.3.1 原码一位乘法 五. 逻辑实现 加法器输入端控制信号：+A、+B 加法器输出端控制信号：1/2∑ A、C、CPA、CPC

  24. 3.1.3.2 补码一位乘法 一. 原则 操作数与结果均以补码表示，连同符号位一起，按相应算法运算。 二. 实现方法： 1.校正法 [XY]补=[X]补[0.Y1Y2……Yn]-[X]补Y0 乘数Y的符号位

  25. 3.1.3.2 补码一位乘法 （1）Y为正： Y补 = 0.Y1Y2……Yn， Y0=0 [XY]补=[X]补[0.Y1Y2……Yn]-[X]补Y0 =[X]补[0.Y1Y2……Yn] （2）Y为负： Y补= 1.Y1Y2……Yn，Y0=1 [XY]补=[X]补[0.Y1Y2……Yn]-[X]补Y0 =[X]补[0.Y1Y2……Yn]-[X]补

  26. -1-2-n = [X]补(-Y0+2 Y1+2 Y2+……+2 Yn) -1-1 -2 =[X]补[-Y0+(Y1-2 Y1)+(2 Y2-2 Y2) -(n-1) -n +……+(2 Yn-2 Yn)] -n -n -n +……+2 （0 -Yn）] +……+2 （Yn+1 -Yn）] +……+2 （Yn+1 -Yn）] -1 -2 -1 -2 = [X]补[(Y1-Y0)+2 (Y2-Y1)+2 (Y3-Y2) = [X]补[(Y1-Y0)+2 (Y2-Y1)+2 (Y3-Y2) 3.1.3.2 补码一位乘法 2.比较法: 展开为部分积的累加和形式： [XY]补=[X]补[0.Y1Y2……Yn]-[X]补Y0

  27. 3.1.3.2 补码一位乘法 若定义[Z0]为初始部分积，[Z1]补……[Zn]补依次为各步求得的累加并右移后的部分积，可将上式改写为： [Z0]补= 0 [Z1]补= 2-1 {[Z0]补+（Yn+1-Yn）[X]补} [Z2]补= 2-1 {[Z1]补+（Yn-Yn-1）[X]补} …… [Zn]补= 2-1 {[Zn-1]补+（Y2-Y1）[X]补} [XY]补= [Zn]补+（Y1-Y0）[X]补

  28. 3.1.3.2 补码一位乘法 三. 比较法算法 • 由于它的操作是乘数相邻两位之差（低位减高位），即两位的比较结果，所以称为比较法。 1.基本操作： 被乘数X补乘以对应的乘数相邻两位之差值再与原部分积累加，然后右移一位，形成该步的部分累加和。

  29. 3.1.3.2 补码一位乘法 Yn(高位) Yn+1(低位)操作(A补为部分积累加和) ( 0 ) 原部分积右移一位1/2A补 原部分积加X补后再右移一位 1/2(A补+X补) 原部分积加[-X]补后再右移一位1/2(A补-X补) 原部分积右移一位1/2A补 0 0 0 1 1 0 1 1 ( 1 ) (-1 ) ( 0 )

  30. 3.1.3.2 补码一位乘法 2.例 X=-0.1101,Y=-0.1011,求(XY)补。 设初值： A=00.0000, B=X补=11.0011, -B=(-X)补=00.1101, C =Y补=1.0101

  31. 步数 条件 操作 A C Cn Cn+1 CnCn+1 00.0000 1.0101 0 1） 1 0 -B + 00.1101 00.1101 00.0110 11.0101 2） 0 1 +B + 11.0011 11.1001 11.1100 111.010 3） 1 0 -B + 00.1101 00.1001 00.0100 1111.01 4） 0 1 +B + 11.0011 11.0111 11.1011 11111.0 5） 1 0 -B + 00.1101

  32. 3.1.3.2 补码一位乘法 4） 0 1 +B + 11.0011 11.0111 11.1011 11111.0 5） 1 0 -B + 00.1101 00.1000 1111 修正 (XY)补= 0.10001111 1.0 : -B修正 0.1 : +B修正 0.0 : 不修正 1.1 : 不修正

  33. 3.1.3.2 补码一位乘法 3.运算规则： (1)A、B取双符号位，符号参加运算； (2)C取单符号位，符号参加移位，以决定最后是否 修正； (3)C末位设置附加位Cn+1，初值为0，CnCn+1组成判 断位，决定运算操作； (4)作n步循环,若需作第n+1步,则不移位,仅修正。

  34. 3.1.3.2 补码一位乘法 4.逻辑实现 加法器输入端控制信号：+A、+B、+B、+1 加法器输出端控制信号：1/2∑ A、C、 ∑ A、CPA、CPC

  35. 3.1.3.3 原码两位乘法 • 每次用两位乘数去乘被乘数。 一.算法分析 Yi(高位) Yi+1(低位) 部分积 累加、移位 0 ( 0 ) 0 0 0 1 1 0 1 1 1/4A 1/4(A+X) 1/4(A+2X) 1/4(A+3X) X ( 1 ) 2X ( 2 ) 3X ( 3 ) 如何实现+3X操作？

  36. 1/4(A-X+4X)=1/4(A-X)+X ① ② 1/4(A+2X+X)=1/4(A+2X)+1/4X ① ② 1/4(A-X+4X)=1/4(A-X)+X ① ② 3.1.3.3 原码两位乘法 • 解决办法： 1/4(A+2X+X)=1/4(A+2X)+1/4X ① ② 1/4(A+3X)= 1/4(A-X+4X)=1/4(A-X)+X ① ② 0 不欠帐 1 欠帐,下次补作+X操作 设置欠帐触发器CJ =

  37. 3.1.3.3 原码两位乘法 二.运算规则 Yi Yi+1 CJ 操 作 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 1/4A 0 CJ 1/4(A+X) 0 CJ 1/4(A+X) 0 CJ 1/4(A+2X) 0 CJ 1/4(A+2X) 0 CJ 1/4(A-X) 1 CJ 1/4(A-X) 1 CJ 1/4A 1 CJ

  38. 3.1.3.3 原码两位乘法 三. 举例 例1. [X]原=1.111111,[Y]原=0.111001,求[XY]原。 解：设初值： A=000.000000， B=|X|=000.111111， 2B=001.111110， -B=111.000001， C = |Y| =00.111001

  39. 步数 条件 操作 A C Cn-1Cn CJ Cn-1CnCJ 000.000000 00.111001 0 1） 0 1 0 +B +000.111111 000.111111 2 000.001111 1100.1110 0 2） 1 0 0 +2B +001.111110 010.001101 2 000.100011 011100.11 0 3） 1 1 0 -B +111.000001 111.100100 2 111.111001 00011100. 1 4） 0 0 1 +B +000.111111 000.111000 000111 还帐 [XY]原=1.111000000111

  40. 3.1.3.3 原码两位乘法 例2. [X]原=0.00111，[Y]原=1.01001,求[XY]原。 解：设初值： A=000.00000, B= |X| =000.00111, 2B=000.01110, -B=111.11001, C =|Y|=00.010010

  41. 3.1.3.3 原码两位乘法 步数 条件 操作 A C Cn-1Cn CJ Cn-1CnCJ 0 0 000.00000 00.01001 1） 1 0 0 +2B +000.01110 000.01110 2 000.00011 1000.0100 0 2） 0 0 0 +0 +000.00000 000.00011 2 000.00000 111000.01 0 3） 0 1 0 +B +000.00111 000.00111 2 000.00001 11111000. 0 [XY]原=1.0000111111

  42. 3.1.3.3 原码两位乘法 四. 运算规则 （1）绝对值相乘，符号单独处理。 （2）A、B取三符号位。 （3）C取双符号位，参加移位；C尾数凑足偶数位。 （4）CJ初值为0，根据每步操作决定其状态，不参 加移位。 （5）作1/2n步循环；若需增加一步，则该步只还 帐，不移位。

  43. 2 加法器输出端控制信号：1/4∑ A、∑ A、C、 CPA、CPC、0 CJ、1 CJ 3.1.3.3 原码两位乘法 五. 逻辑实现 加法器输入端控制信号：+A、+B、+2B、+B、+1

  44. 3.1.3.4 补码两位乘法 补码两位乘法是在补码一位乘法算法拓展来的。 以补码一位乘法中， [Z1]补 、[Z2]补两个部分积为例讨论： [Z1]补 = 2-1 {[Z0]补 +（Yn+1-Yn）[X]补} [Z2]补 = 2-1 {[Z1]补 +（Yn-Yn-1）[X]补} 将[Z1]补代入[Z2]补得： [Z2]补 = 2-1 {2-1 [[Z0]补+ (Yn+1– Yn ) [X]补] + (Yn– Yn-1 ) [X]补} = 2-2 [[Z0]补+ (Yn+1– Yn ) [X]补] + 2-1 [(Yn– Yn-1 ) [X]补] = 2-2 [[Z0]补+ (Yn+1– Yn ) [X]补] + 2-2 [(2Yn– 2Yn-1 ) [X]补] = 2-2 [[Z0]补+ (Yn+1– Yn ) [X]补+ (2Yn– 2Yn-1 ) [X]补] = 2-2 [[Z0]补+ (Yn+1– Yn + 2Yn– 2Yn-1 ) [X]补] = 2-2 [[Z0]补+ (Yn+1 + Yn– 2Yn-1 ) [X]补] 可见，求[Z2]补需要将前次部分积加(Yn+1 + Yn– 2Yn-1 ) [X]补，最后再右移2位。所以需对Yn+1 Yn Yn-1三位做判断。

  45. 3.1.3.4 补码两位乘法

  46. 3.1.4 定点除法运算 • 手算除法 例：X= 0.10110，Y = 0.11111，求X/Y = ？ 0. 1 0 1 1 0 0.11111 0.10110 0 11111 实现除法的关键： 比较余数、除数 绝对值大小，以 决定上商。 1101 0 0 11111 10101 0 11111 0. 00000 1011 0 . . -5 商： 0.10110 余数：0.10110×2

  47. 3.1.4 定点除法运算 1、由手算除法过程可知：取绝对值相除，即判断X > Y ? ， 若X > Y ，则商1，否则商0。每一步都是余数末位后面补0与除数比较。 2、改进成计算机算法的问题： 1）如何判断够减? 将心算比较改为减法比较，减Y 用加 [- Y]补实现。 2）将余数末位后面补0改为左移余数。使商在一个位置固定进行。导致正确的余数应为rn . 2-n。 3）符号? 原码除法符号单独处理，补码除法符号参与运算。

  48. 3.1.4.1 原码不恢复余数除法 • 恢复余数算法思想: 比较两数大小可用减法试探。 为正:够减,商1。 为负:不够减,商0,恢复原余数。 2×余数-除数=新余数

  49. 3.1.4.1 原码不恢复余数除法 一.算法分析 第一步:2r1-B=r2’<0 第二步:r2’+B=r2(恢复余数) 第三步:2r2-B=r3 第一步:2r1-B=r2<0 第二步:2r2+B=r3 (不恢复余数) 2r2-B=2(r2’+B)-B =2r2’+B=r3

  50. 3.1.4.1 原码不恢复余数除法 二. 算法 ri为正，则Qi为1，第i+1步作2ri-Y； ri为负，则Qi为0，第i+1步作2ri+Y。 每步操作后， 1）如果余数为正，商1，余数左移1位，减去除数， 2）如果余数为负，商0，余数左移1位，加上除数。

More Related