1 / 11

Mastering Indexes for Efficient Data Searching

Learn about 2-level indexes, primary purposes, structures, algorithms, search optimization, and best practices for managing indexed files effectively. Explore examples and strategies to improve searching and minimize memory usage. Dive into levels, key arrangements, and algorithms to enhance data retrieval processes.

nardo
Download Presentation

Mastering Indexes for Efficient Data Searching

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. 2 Level Indexes Indexed Files - Part Two Portions of this lecture stolen from Foster's 325 Lecture Notes

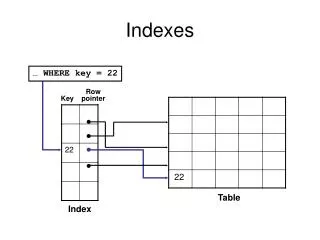
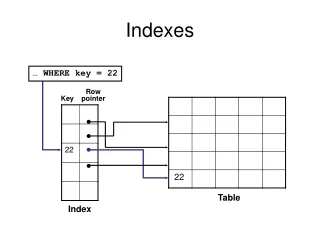
  2. Where we left off last class The primary purpose of using indexes is to speed searching. In a single layer indexed file, the index-to-data relationship is 1:1. The index resides in main memory for fast access. What if that 1:1 index is too big for memory?

  3. 2 Levels of Indexes First Level Index • resides in memory • entries point to the Second Level • entries are ordered for fast searching • entries contain • key • an IRRN - Index Relative Record Number (pointer into the Second Level) • size is TBD Second Level Index • entirety stays in a file • 1:1 ratio of entries to records in data file • entries are ordered for fast searching • entries contain • key • DRRN - Data RRN (pointer into the data file)

  4. An Overly Simple Example

  5. Search Algorithm Can this be a binary search? Data Size = N records Level One Size = K1 entries Preconditions : K2 = N / K1 level one index is already in an array in memory (arrary1) i = 0; while (Target > array1[i].Key) && (i < K1) i++; i = i-1; SeekG (secondaryfile, array1[i].IRRN*sizeof(index records)) Read (secondaryfile, K2 records, into array2) binary search array2 for Target SeekG (datafile, array2[location].DRRN*sizeof(data records)) read record from datafile

  6. A Better Example

  7. Add Algorithm YIKES! Sorting a File takes a long time! Append new record to end of datafile add entry (Key and DRRN) to end of secondary file sort secondary key K2 = N / K1 for (i=0; i<K1; i++) array1[i].key = secondarykey(i * K2) array1[i].IRRN = i * K2

  8. Better Structure when Additions are Frequent • Instead of filling the secondary index, leave room for expansion. • Example • between Adams and Foster, put 15 names instead of 20 • that leaves 5 growth spots before an adjustment is needed • when adding "Baker", only need to sort (move) Adams to Foster-1

  9. Theoretical Best Size of Index 1 • Remember: • Level 1 index stays in memory • only a portion of Level 2 goes into memory • To minimize search times of those two arrays, optimal size of Index 1 is sqrt(N) • Example • Assume N = 100 • Size of Level 1 = sqrt(100) = 10 • each of those level 1 entries points to 10 level 2 entries • so we end up searching two arrays of 10 elements each

  10. Real Best Size of Index 1 "To minimize search times of those two arrays, optimal size of Index 1 is sqrt(N)" But array2 must be read from a file over and over and over. So, the smaller array2 the better! Hence, optimal size of Index 1 = as big as main memory allows

  11. Next Class • Multiple Indexes • multiple keys • maybe you and I should not see the same items • 3 Levels of Indexes

More Related