Optimization and Stability in Games with Restricted Interactions
290 likes | 403 Views
This paper explores the dynamics of coalitional games with restricted cooperation, focusing on the Cost of Stability (CoS) within different game structures. It delves into essential concepts such as superadditivity, weighted voting games, and the implications of restricted coalitions due to underlying communication networks. The main results include tight bounds on the CoS, highlighting conditions under which stable outcomes can be achieved. The research emphasizes the importance of subsidies and external payments in stabilizing games and discusses computational complexity in determining stable coalition structures.

Optimization and Stability in Games with Restricted Interactions
E N D
Presentation Transcript
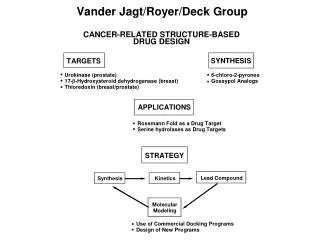
Optimization and Stability in Games with Restricted Interactions Reshef Meir, YairZick and Jeffrey S. Rosenschein CoopMAS 2012
Lecture content • Coalitional (TU) games • Restricted cooperation • The Cost of Stability • Main result: a bound on the CoS • Discussion
TU Games - Notations • Agents: N= (1,…,n) • Coalition: S µ N • Characteristic function: v: 2I→ R • A TU game is simple, if every coalition either wins or loses, i.e. v: 2I→ {0,1} • A TU game is monotone, if the value of a coalition can only increase by adding more agents to it
TU Games – notations (2) • A TU game is superadditive (SA), if there is positive synergy. That is, v(S[ T) ≥ v(S) + v(T) for disjoint S,T. • No need to consider coalition structures • Results can be generalized • Every game has a superadditive cover
Weighted Voting Games (WVG) A class of simple TU games Each agent has a weight wi2 R A game has a quota q 2 R G = [w1,w2,…,wn;q] A coalition Swins if Σi2Swi¸q
Payoffs • Agents may freely distribute profits. • An imputation is a vector x = (x1,…,xn) such that Σi2Nxi= v(N) • Individual rationality: each agent gets at least what she can make on her own: xi≥v({i}) • The payoff of a coalition x(S) is the sum of payments to its agents.
The Core • The coreis the set of all stable imputations: for all S µ N we haveΣi2S xi¸ v(S) • May be empty in many games: • No stable imputations • Example: G = [2,2,3;4] • Computational questions: • Is the core empty? • Is the vector x in the core?
Restricted cooperation • Some coalitions may be impossible or unlikely due to practical reasons • an underlying communication network (Myerson’77). • agents are nodes. • A coalition can form only if its agents are connected. 1 2 4 9 11 3 5 6 10 8 12 7
Restricted cooperation - example • The coalition {2,9,10,12} is allowed • The coalition {3,6,7,8} is not allowed 1 2 4 9 11 3 5 6 10 8 12 7
Restricted cooperation increases stability Theorem [Demange’04] : If the underlying communication network H is a tree, then the core is non-empty. Moreover, a core imputation can be computed efficiently. 1 2 4 9 11 3 5 6 10 8 12 7
What if the core is empty? • A solution: subsidies • Sometimes an external partyis interested in the stability of a specific outcome • Willing to spend money to increase stability
External Payments v(N) • Originally, we divided v(N)between the agents. • We increase the value of v(N), creating a “superimputation”: • Division of the incremented value v’(N)= α∙v(N) • Create a new game G(α)
The Cost Of Stability (CoS) (Bachrach et al., SAGT’09) • Observation: With a big enough payment, every game can be stabilized • α ≤ n • The Cost of Stability (CoS) is the minimal subsidy αthat stabilizes the grand coalition i.e. allows a non-empty core in G(α) • Can also stabilize coalition structures
Back to our example • G = [2,2,3;4] (core is empty) • By distributing a total payoff of 1½ (rather than 1), the core of G(1½) is non-empty. • x = (½, ½, ½) is a stable super-imputation. • Thus CoS(G) ≤ 1½ • Is this bound tight? • A lower payment cannot stabilize the game • Thus CoS(G) = 1½
Conceptual Issues • How do properties of the game affect the CoS? • Superadditivity, restricted cooperation, convexity… • Can we stabilize other outcomes? • A particular coalition, coalition structures…
Computational Issues • How hard is computing the optimal coalitional structure? • How hard is computing the CoS? • How hard is checking whether a specific super-imputation is stable? • The answer depends on game representation • We assume oracle access to v(S)
Previous work Bounds on the CoS • In the general case can be as high as n • For example, the WVG [1,1,1,…,1; 1] • If G is superadditive, CoS(G)≤√n • Easier to achieve cooperation • If G is superadditive and symmetric, CoS(G) ≤ 2 Bachrach et al., SAGT’09 Meir et al., SAGT ‘10
Previous work CoS with restricted cooperation • Recall that by [Demange’04] : if H is a tree, then the core is non-empty (i.e. CoS= 0). • Sparse graphs lower subsidies? • Sparse graphs easier computation? Theorem: If Hcontains a single cycle, then CoS(G) ≤ 2, and this is tight Meir et al., IJCAI ‘11
Graphs and tree-width • Combinatorial measures to the “cyclicity” of a graph: • Degree • Path-width • Tree-width • … • Many NP-hard combinatorial problems become easy when the tree-width is bounded. 1 2 4 9 11 3 5 10 6 8 7 1,2,3 2,4 2,5,9 5,9,10 5,6,8 6,7,8 9,11 5,8,10
Bounding the CoS Conjecture [MRM’11]: Let d be the maximal degree in H, then CoS(G) ≤ d There are games on a 3-dimensional grid (d = 6) with unbounded CoS Conjecture (fixed): Let k be the tree-width of H, then CoS(G) ≤ k
Main result Theorem: Let G be a superadditivegame, then CoS(G) ≤ (TW(H) + 1) ∙ log(n) Also, a stable payoff vector can be found efficiently
Proof a b x y z … a b c d a b e f c d i j b c k a d l m
Proof a b x y z … a b c d a b e f c d i j b c k a d l m (k+1)v(N)
Proof a b x y z … a b c d a b e f c d i j b c k a d l m (k+1)v(N)
Proof a b x y z … a b c d a b e f c d i j b c k a d l m f x z i j … (k+1)v(N) + (k+1)(v(S1) + v(S2) + …) ≤ (k+1)v(N) + (k+1)v(N) + …
Proof a b x y z … a b c d a b e f c d i j b c k a d l m f x z i j … We pay at most (k+1)v(N) at each iteration
Proof a b x y z … a b c d a b e f c d i j b c k a d l m f x z i j … We repeat at mostlog(|T |) ≤ log(n) times
Discussion • The CoS depends on the tree-width of the underlying graph • New results… • Bounded tree-width does not facilitate computations (e.g. Greco et al.’11)
Thank You For more information: http://www.huji.ac.il/~reshef24