1 / 26

3.3.1 几何概型

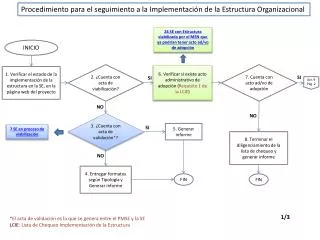
3.3.1 几何概型. 探究几何概型. 复习回顾， 情景引入 探索归纳，领悟概念 巩固深化，应用拓展 总结评价，促进成长. 复习回顾. 古典概型的两个基本特征 ?. 有限性 : 在一次试验中 , 可能出现的结果只有有限个 , 即只有有限个不同的基本事件； 等可能性 : 每个基本事件发生的可能性是相等的. 计算概率. 上海世博会圆满闭幕，某玩具厂商为推销其生产的吉祥物玩具，扩大知名度，特举办了一次有奖活动：顾客随意掷两颗骰子，如果点数之和大于 10 ，则可获得一个海宝玩具，问顾客能得到一个海宝玩具的概率是多少？. 特征： 基本事件有限 基本事件等可能出现.

lee
Download Presentation

3.3.1 几何概型

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. 3.3.1 几何概型

  2. 探究几何概型 • 复习回顾，情景引入 • 探索归纳，领悟概念 • 巩固深化，应用拓展 • 总结评价，促进成长

  3. 复习回顾 古典概型的两个基本特征? • 有限性:在一次试验中,可能出现的结果只有有限个,即只有有限个不同的基本事件； • 等可能性:每个基本事件发生的可能性是相等的.

  4. 计算概率 上海世博会圆满闭幕，某玩具厂商为推销其生产的吉祥物玩具，扩大知名度，特举办了一次有奖活动：顾客随意掷两颗骰子，如果点数之和大于10，则可获得一个海宝玩具，问顾客能得到一个海宝玩具的概率是多少？ 特征： 基本事件有限 基本事件等可能出现 设“顾客得到海宝玩具”为事件A P(A)=3/36=1/12 结论：为古典概型

  5. 计算概率 厂商为了增强活动的趣味性，改变了活动方式，设立了一个可以自由转动的转盘（如图1）转盘被等分成8个扇形区域.顾客随意转动转盘，如果转盘停止转动时，指针正好指向灰色区域，顾客则可获得一套海宝玩具.问顾客能得到一套海宝玩具的概率是多少？ 特征： 基本事件有无限个 每个基本事件等概率出现 不是古典概型 如何计算概率呢？

  6. 一、创设情景，引入新课 　　在转盘游戏中，当指针停止时，指针指向哪种颜色区域的可能性大？ 红色区域对应的圆弧长，所以指针指在红色的区域可能性大。 指针停止时 指向了圆弧上的一点

  7. 二、主动探索，领悟归纳 • 问题:甲乙两人玩转盘游戏,规定当指针指向B区域时,甲获胜,否则乙获胜. 求甲获胜的概率是多少? • 点击右侧的小转盘，更换一个转盘后，甲获胜的概率是多少？

  8. 主动探索 • 事实上,甲获胜的概率与字母B所在扇形区域的弧长有关,而与字母B所在区域的位置无关. 上述问题中，基本事件有无限多个，虽然类似于古典概型的“等可能性”还存在，但显然不能用古典概型的方法求解，怎么办呢？

  9. 星星可能的落点有无数个 基本事件无数个 星星落在区域内每一点上的可能性相同 基本事件等概率 主动探索 • 向图中区域内投掷星星，计算星星落在红色区域的概率 化物为点 • 事实上,落在红色区域的概率与红色区域的面积有关,而与该区域的位置无关.

  10. 领悟归纳 对于一个随机试验 • 每个基本事件几何区域内随机地取一点 （该区域中每一点被取到是等可能的） • 一个随机事件的发生 取到区域内的某个指定区域中的点. • 这里的区域可以是长度，面积，体积等。用这种方法处理随机试验，称为几何概率模型。

  11. 领悟归纳 • 如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例,则称这样的概率模型为几何概率模型,简称为几何概型. 几何概型

  12. 领悟归纳 • 几何概型的特点: (1)试验中所有可能出现的结果(基本事件)有无限多个. (2)每个基本事件出现的可能性相等. • 在几何概型中,事件A的概率的计算公式如下: 概率等于零的一定是不可能事件吗？ 不可能事件 ，概率一定为0 反之不成立

  13. 三、巩固深化，应用拓展 几何概型的计算 一个质地均匀的陀螺的圆周上均匀地刻有[0 , 5)上诸数字，在桌面上旋转它，求当它停下来时，圆周与桌面接触处的刻度位于区间 [2 , 3] 上的概率。 = [2 , 3] = 3-2 = 1 = 5- 0 = 5

  14. 应用拓展 例：某商场为了吸引顾客，设立了一个可以自由转动的转盘，并规定:顾客每购买100元的商品，就能获得一次转动转盘的机会。如果转盘停止时，指针正好对准红、黄或绿的区域，顾客就可以获得100元、50元、20元的购物券（转盘等分成20份） 甲顾客购物120元，他获得购物券的概率是多少？他得到100元、50元、20元的购物券的概率分别是多少？

  15. 甲顾客购物的钱数在100元到200元之间，可以获得一次转动转盘的机会，转盘一共等分了20份，其中1份红色、2份黄色、4份绿色，因此对于顾客来说：甲顾客购物的钱数在100元到200元之间，可以获得一次转动转盘的机会，转盘一共等分了20份，其中1份红色、2份黄色、4份绿色，因此对于顾客来说： P（获得购物券）= P（获得100元购物券）= 1/20 P（获得50购物券）= P（获得20购物券）=

  16. 解:设A={等待的时间不多于10分钟}.我们所 关心的事件A恰好是打开收音机的时刻位于 [50,60]时间段内,因此由几何概型的求概率 的公式得 即“等待的时间不超过10分钟”的概率为 例1某人午觉醒来,发现表停了,他 打开收音机,想听电台报时,求他等待的时间不多于10分钟的概率. 分析：假设他在0－60分钟之间任何一个时刻打开收音机是等可能的，但0－60之间有无穷个时刻，不能用古典概型的公式计算随机事件发生的概率。 可以通过几何概型的求概率公式得到事件发生的概率。

  17. 7 设“等车时间不超过3分钟”为事件A 巩固练习 假设车站每隔 10 分钟发一班车，随机到达车站，问等车时间不超过 3 分钟的概率 ？ 0← →10

  18. 学法领悟 • 对于复杂的实际问题,解题的关键是要建立模型,找出随机事件与所有基本事件相对应的几何区域,把问题转化为几何概率问题,利用几何概率公式求解.

  19. 练习 5.取一根长为3米的绳子,拉直后在任意位置剪断,那么剪得两段的长都不少于1米的概率有多大? 1m 1m 3m 解：如上图，记“剪得两段绳子长都不小于1m”为事件A，把绳子三等分，于是当剪断位置处在中间一段上时，事件A发生。由于中间一段的长度等于绳子长的三分之一，所以事件A发生的概率P（A）=1/3。

  20. 练习 解：设“汽车在1～3分钟之间到达”为事件A，则 所以“汽车在1～3分钟之间到达”的概率为 1.公共汽车在0～5分钟内随机地到达车站，求汽车在1～3分钟之间到达的概率。 分析：将0～5分钟这段时间看作是一段长度为5 个单位长度的线段，则1～3分钟是这一线段中 的2个单位长度。

  21. 练习 2.有一杯1升的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1升,求小杯水中含有这个细菌的概率. 3.如右图,假设你在每个图形上随机撒一粒黄豆,分别计算它落到红色部分的概率.

  22. 练习 4.一张方桌的图案如图所示。将一颗豆子随机地扔到桌面上，假设豆子不落在线上，求下列事件的概率： （1）豆子落在红色区域； （2）豆子落在黄色区域； （3）豆子落在绿色区域； （4）豆子落在红色或绿色区域； （5）豆子落在黄色或绿色区域。

  23. 练习 M 6.在等腰直角三角形ABC中，在斜边AB上任取一点M，求AM小于AC的概率。 分析：点M随机地落在线段AB上，故线段AB为区域D。截取AC’=AC,当点M位于图中的线段AC’上时，AM＜AC，故线段AC’即为区域d。 C 解： 在AB上截取AC’=AC，于是 P（AM＜AC）=P（AM＜AC’） A B C’ 则AM小于AC的概率为

  24. 练习 7.在半径为1的圆上随机地取两点，连成一条线，则其长超过圆内等边三角形的边长的概率是多少？ B 解：记事件A={弦长超过圆内接 等边三角形的边长}，取圆内接 等边三角形BCD的顶点B为弦 的一个端点，当另一点在劣弧 CD上时，|BE|>|BC|，而弧CD 的长度是圆周长的三分之一， 所以可用几何概型求解，有 . 0 C D E 则“弦长超过圆内接等边三角形的边长”的概率为

  25. 四、总结评价，促进成长 • 1.几何概型的特点. • 2.古典概型与几何概型的区别： 1）两种模型的基本事件发生的可能性都相等； 2）古典概型要求基本事件是有限个，而几何概型则要求基本事件有无限多个。 • 3.几何概型的概率公式及运用.

  26. 谢谢

More Related