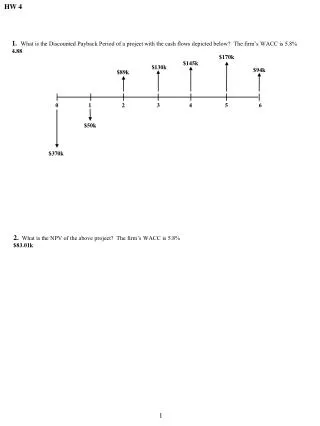
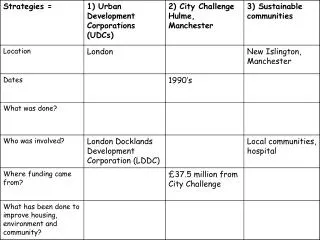
HW 13
350 likes | 594 Views
HW 13. 100071021. Prime Number Generator. if isPrime == 1 most = most + 1; Primes(most) = test; end if most >= num break; end test = test + 1; end end. function Primes = getPrime ( num ) Primes = zeros (num,1); Primes(1) = 2; test = 3;

HW 13
E N D
Presentation Transcript
HW 13 100071021
Prime Number Generator if isPrime == 1 most = most + 1; Primes(most) = test; end if most >= num break; end test = test + 1; end end function Primes = getPrime( num) Primes = zeros(num,1); Primes(1) = 2; test = 3; most = 1; while 1 test_ub = ceil(sqrt(test)); isPrime = 1; for i = 1 : most if test_ub < Primes(i) break; end if mod(test,Primes(i))==0 isPrime = 0; break; end end
Halton Path function SPaths =HaltonPaths( S,mu,sigma,T,NSteps,NRepl ) NRepl = 2*ceil(NRepl/2); dt = T/NSteps; nudt = (mu-0.5*sigma^2)*dt; sidt = sigma*sqrt(dt); RandMat = zeros(NRepl, NSteps); seeds = getPrime(2*NSteps); for i = 1 : NSteps H1 = Halton(NRepl/2,seeds(i*2-1)); H2 = Halton(NRepl/2,seeds(i*2)); Vlog = sqrt(-2*log(H1)); Norm1 = Vlog .* cos(2*pi*H2); Norm2 = Vlog .* sin(2*pi*H2); RandMat(:,i) = [Norm1 Norm2]; end Increments = nudt + sidt*RandMat; Init = log(S) * ones(NRepl,1); LogPath = cumsum( [Init , Increments], 2 ); SPaths = exp(LogPath); end
Asian Option (Monti Carlo) function [ call, put, cci, pci ] = AsianMC( S,K,r,sigma,T,mode,NSample,NRepl,Rtype ) % mode 0=>use ST 1=>use K % Rtype 0=>rand 1=>Halton % call=>ST(K)-A put=>A-ST(K) Payoffs = zeros(NRepl,2); if Rtype == 0 Paths = AssetPaths(S,r,sigma,T,NSample,NRepl); else Paths = HaltonPaths(S,r,sigma,T,NSample,NRepl); end
for i = 1 : NRepl if mode == 0 Payoffs(i,:) = [ max(0, Paths(i,NSample+1)-mean(Paths(i,2:NSample+1)) ) , max(0, mean(Paths(i,2:NSample+1)-Paths(i,NSample+1)) ) ]; else Payoffs(i,:) = [ max(0, K-mean(Paths(i,2:NSample+1)) ) , max(0, mean(Paths(i,2:NSample+1)-K) ) ]; end end [call aux cci] = normfit( exp(-r*T)*transpose(Payoffs(:,1)) ); [put aux pci] = normfit( exp(-r*T)*transpose(Payoffs(:,2)) ); end
Demo Code S = 50; K = 50; r = 0.1; T = 5/12; sigma = 0.4; NSample= 5; NRepl= 1000; lim = 1000; for i = 1 : lim [STrand(i), a, b, d ] = AsianMC( S,K,r,sigma,T,0,NSample,i,0 ); STrandci(i) = b(2)-b(1); [SThal(i), a, b, d ] = AsianMC( S,K,r,sigma,T,0,NSample,i,1 ); SThalci(i) = b(2)-b(1); [Krand(i), a, b, d ] = AsianMC( S,K,r,sigma,T,1,NSample,i,0 ); Krandci(i) = b(2)-b(1); [Khal(i), a, b, d ] = AsianMC( S,K,r,sigma,T,1,NSample,i,1 ); Khalci(i) = b(2)-b(1); end
STrand(1000) SThal(1000) Krand(1000) Khal(1000) ans = 2.9223 ans = 3.1876 ans = 2.6753 ans = 2.7760
figure; plot(1:lim,STrand,1:lim,Krand); legend('ST - A','K - A'); title('ST vs K (Rand)');
figure; plot(1:lim,SThal,1:lim,Khal); legend('ST - A','K - A'); title('ST vs K (Halton)');
figure; plot(1:lim,STrand,1:lim,SThal); legend('Rand','Halton'); title('Random vs Halton (ST - A)');
figure; plot(1:lim,Krand,1:lim,Khal); legend('Rand','Halton'); title('Random vs Halton (K - A)');
figure; plot(1:lim,STrandci,1:lim,SThalci); legend('Rand','Halton') title('CI of (ST - A)')
figure; plot(1:lim,Krandci,1:lim,Khalci); legend('Rand','Halton') title('CI of (K - A)')
Lookback Option function [ call, put, cci, pci ] = LookBackMC( S,r,sigma,T,mode,NSample,NRepl,Rtype ) % mode 0=>use Smax 1=>use Smin % Rtype 0=>rand 1=>Halton % call=>ST-Sm put=>Sm-ST Payoffs = zeros(NRepl,2); if Rtype == 0 Paths = AssetPaths(S,r,sigma,T,NSample,NRepl); else Paths = HaltonPaths(S,r,sigma,T,NSample,NRepl); end
for i = 1 : NRepl if mode == 0 Payoffs(i,:) = [ max(0, Paths(i,NSample+1)-max(Paths(i,2:NSample+1)) ) , max(0, max(Paths(i,2:NSample+1)-Paths(i,NSample+1)) ) ]; else Payoffs(i,:) = [ max(0, Paths(i,NSample+1)-min(Paths(i,2:NSample+1)) ) , max(0, min(Paths(i,2:NSample+1)-Paths(i,NSample+1)) ) ]; end end [call aux cci] = normfit( exp(-r*T)*transpose(Payoffs(:,1)) ); [put aux pci] = normfit( exp(-r*T)*transpose(Payoffs(:,2)) ); end
Demo Code S = 50; K = 50; r = 0.1; T = 5/12; sigma = 0.4; NSample= 5; NRepl= 1000; lim = 1000; for i = 1 : lim [a, Maxrand(i), d, b ] = LookBackMC( S,r,sigma,T,0,NSample,i,0 ); Maxrandci(i) = b(2)-b(1); [a, Maxhal(i), d, b ] = LookBackMC( S,r,sigma,T,0,NSample,i,1 ); Maxhalci(i) = b(2)-b(1); [Minrand(i), a, b, d ] = LookBackMC( S,r,sigma,T,1,NSample,i,0 ); Minrandci(i) = b(2)-b(1); [Minhal(i), a, b, d ] = LookBackMC( S,r,sigma,T,1,NSample,i,0 ); Minhalci(i) = b(2)-b(1); end
Maxrand(1000) Maxhal(1000) Minrand(1000) Minhal(1000) ans = 5.5906 ans = 5.5884 ans = 7.1912 ans = 7.2195
figure; plot(1:lim,Maxrand,1:lim,Minrand); legend('Smax - ST','ST - Smin'); title('ST vs K (Rand)');
figure; plot(1:lim,Maxhal,1:lim,Minhal); legend('Smax - ST','ST - Smin'); title('ST vs K (Halton)');
figure; plot(1:lim,Maxrand,1:lim,Maxhal); legend('Rand','Halton'); title('Random vs Halton (Smax - ST)');
figure; plot(1:lim,Minrand,1:lim,Minhal); legend('Rand','Halton'); title('Random vs Halton (ST - Smin)');
figure; plot(1:lim,Minrandci,1:lim,Minhalci); legend('Rand','Halton') title('CI of (Smax - ST)')
figure; plot(1:lim,Maxrandci,1:lim,Maxhalci); legend('Rand','Halton') title('CI of (ST - Smin)')