1 / 12

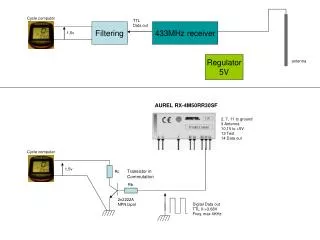
Particle Filtering

This work explores the integration of Dynamic Belief Networks (DBNs) and Particle Filtering (PF) for probabilistic inference in complex systems. Utilizing a two-stage influence diagram, we investigate how to compute probabilities over time while addressing challenges such as non-linearity and high-dimensional spaces. The document highlights the Rao-Blackwellisation technique to improve estimation efficiency, demonstrating its use in filtering density and approximating posterior distributions in DBNs. Key insights into the advantages and limitations of PF are discussed, offering guidance for practical applications.

inez
Download Presentation

Particle Filtering

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Particle Filtering ICS 275b 2002

  2. Dynamic Belief Networks (DBNs) Interaction graph Two-stage influence diagram

  3. Notation t=0 t=1 t=2 t=1 t=2 X0 X1 X2 Xt Xt+1 Xt – value of X at time t X 0:t ={X0,X1,…,Xt}– vector of values of X Yt – evidence at time t Y 0:t = {Y0,Y1,…,Yt} Y0 Y1 Y2 Yt Yt+1 DBN 2-time slice

  4. Query • Compute P(X 0:t |Y 0:t ) or P(X t |Y 0:t ) • Hard!!! over a long time period • Approximate! Sample!

  5. Particle Filtering (PF) • = “condensation” • = “sequential Monte Carlo” • = “survival of the fittest” • PF can treat any type of probability distribution, non-linearity, and non-stationarity; • PF are powerful sampling based inference/learning algorithms for DBNs.

  6. Particle Filtering

  7. Example Particlet={at,bt,ct}

  8. PF Sampling Particle (t) ={at,bt,ct} Compute particle (t+1): Sample bt+1, from P(b|at,ct) Sample at+1, from P(a|bt+1,ct) Sample ct+1, from P(c|bt+1,at+1) Weight particle wt+1 If weight is too small, discard Otherwise, multiply

  9. Drawback of PF • Drawback of PF • Inefficient in high-dimensional spaces (Variance becomes so large) • Solution • Rao-Balckwellisation, that is, sample a subset of the variables allowing the remainder to be integrated out exactly. The resulting estimates can be shown to have lower variance. • Rao-Blackwell Theorem

  10. Problem Formulation • Model : general state space model/DBN with hidden variables ztand observed variables yt • Objective: • or filtering density • To solve this problem,one need approximation schemes because of intractable integrals

  11. Rao-Blackwellised PF • Divide hidden variables into two groups: rt and xt • Assume conditional posterior distribution p(x0:t | y1:t ,r0:t ,) is analytically tractable • We only need to focus on estimating p(r0:t | y1:t), which lies in a space of reduced dimension:

  12. Particle Filtering and Rao-Blackwellisation • Monte Carlo integration

More Related