Quantum Physics and Nuclear Physics
790 likes | 1.45k Views
Quantum Physics and Nuclear Physics. 13.1 Quantum Physics. Quantum Physics Revision When an electron falls to a lower energy level , the change in energy ( Δ E) is emitted as a photon of e-m radiation. . Δ E = E 2 – E 1

Quantum Physics and Nuclear Physics
E N D
Presentation Transcript
Quantum Physics and Nuclear Physics 13.1 Quantum Physics
Quantum Physics • Revision • When an electron falls to a lower energy level, the change in energy (ΔE) is emitted as a photon of e-m radiation. • ΔE = E2 – E1 • The change in energy is proportional to the frequency of the emitted photon: • ( E = Photon energy • h = Plank’s constant • = 6.6 x 10-34 m2kgs-1 ) E = hf
E.g. Energy levels in the hydrogen atom: Thus the emission spectrum for Hydrogen (this shows only the visible section)...
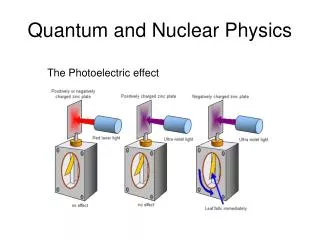
The Photoelectric Effect • Demo: • u.v. light shone onto a zinc plate will cause a negative charged electroscope to discharge . • visible light will not cause it to discharge (even if very intense). • if the charge is positive, even the u.v. will not cause it to discharge.
Conclusion • u.v. light causes negative electrons to be emitted from the surface of zinc (this is called photoelectric emission) but visible light does not, hence the first two observations. • if u.v. causes negative electrons to be emitted, the positive charge will not be discharged. Applet link
Threshold Frequency Electrons will only be emitted from zinc by photoelectric emission if the electromagnetic radiation incident upon its surface has a frequency of 1 x 1015 Hz or above. This is called the threshold frequency of zinc. Limitation of Wave Theory of Light Wave theory would suggest that once enough visible light energy had been absorbed by the zinc, the electron would be able to escape. This is not the case. No matter how intense the incident radiation, if its frequency is below the threshold frequency for a particular material, no photoelectric emission will occur.
Photons – the Quantum Model • In 1900 Max Planck came up with the idea of energy being ‘quantised’ in some situations. i.e. existing in small ‘packets’. • In 1905 Einstein suggested that all e-m radiation is emitted in small quanta called photons rather than in a steady wave. • Intensity of radiation depends on the number of photons being emitted per second (not amplitude as suggested by the wave model). • Energy per photon depends upon its frequency: E = hf
Work Function and Photoelectric Emission When u-v light is incident upon a zinc surface, each photon gives its energy to a single electron on the zinc surface. u-v photons have a high frequency. As a result they give enough energy to the electron to escape from the surface. The minimum energy needed to just remove an electron from a metal surface is called the work function, .
Low intensity u-v light will still cause electrons to be emitted. Because there are less photons per second there will be less electrons emitted per second. If the incident light has a lower frequency, each photon has less energy and so no electrons are emitted, irrespective of the intensity.
Einstein’s Photoelectric Equation If the photon energy (E=hf) is greater than the work function (), any remaining energy becomes kinetic energy of the electron (= ½mv2). Thus Einstein stated... This is one version of Einstein's photoelectric equation. hf = + ½ mv2 m = mass of an electron v = speed of fastest electrons (ms-1)
Einstein’s theory was confirmed by Robert Millikan in 1916. He realised that if the clean metal emitting surface was given a positive potential, the electron emission could be stopped. Thus, if the p.d. applied was known, the KE ‘removed’ from the fastest electron can be found: We know... V = W / q W = eV So... Link - PhET simulation V = stopping voltage e = charge on an electron = 1.6 x 10-19C = Work function (Joules) hf = + eV
Testing Einstein's Photoelectric Equation • Einstein’s photoelectric equation can be rearranged to give... • Thus plotting a graph of V against f enables us to determine Plank’s constant. V = h f - e e
Incident radiation is shone onto a photoelectric cell with a low work function • This causes electrons to be emitted from the larger emitting electrode. If they reach the small receiving electrode a current is detected on the ammeter • The stopping voltage V is increased until zero current flows through the ammeter. The p.d. has made it impossible for even the fastest electrons to escape from the large electrode. • The experiment is repeated with different frequency incident radiation and a set of values for frequency and stopping voltage are collected.
Q. Explain why this graph will always have the same gradient, whatever metal is used for the emitting electrode. Q. Explain how you would determine a value for the work function of the metal used to produce the graph above. Q.
Photocurrents If the metal surface and frequency of incident radiation are both kept constant, a graph can be plotted showing how the photoelectric current (photocurrent) in a photocell varies with applied p.d. (voltage). Consider these situations and explain the photocurrent that will flow in each case: + - - +
0 + Photocurrent Applied p.d. Saturation current Stopping potential, Vs
0 + Photocurrent Applied p.d. High intensity Low intensity
0 + Photocurrent Applied p.d. Low frequency (red) Higher frequency (blue)
The Wave Nature of Matter We have seen that light behaves both like a wave (it diffracts) and like a particle (in explaining photoelectric emission). It has wave particle duality. Demo 1: Shine a beam of laser light (a wave) through a single diffraction grating (like a very fine gauze) then through many gratings crossed at angles to each other. Demo 2: Fire a beam of electrons (particles of matter) at a thin piece of graphite using a cathode ray tube. Wave - particle duality is the ability of something to exhibit both wave and particle behaviour.
Control grid Anode Cathode Graphite foil Flourescent screen VA
De Broglie’s Equation Considering a photon of light, in 1924 Prince Louis Victor de Broglie equated Einstein’s mass-energy relation and Planck’s equation: E = mc2 and E = hf thus... mc2 = hf so... mc2 = h c λ so... or But c = f λ λ = h mc λ = h p
This is the de Broglie equation. ( Where h = Planck’s constant = 6.6 x 10-34Js ) By analogy, this equation can be applied to any other particle of matter. Thus de Broglie’s Hypothesis: Q1 A year 13 student runs with joy to his physics lesson. If he runs at 5 ms-1 and has mass 60kg, determine the de Broglie wavelength of his motion. Comment upon your answer. All matter can behave like a wave, with the wavelength given by Plank’s constant divided by the matter’s momentum.
Q2 An electron is accelerated in a cathode ray tube through a potential difference of 2kv. • Determine the velocity of the electron (me = 9.11 x 10-31 kg) • 2.65 x 107 ms-1 • Determine the de Broglie wavelength of the electron. • 2.7 x 10-11 m
Energy Levels E.g. h = Planck constant = 6.6 x 10-34 m2kgs-1 E = hf hf = E2 - E1
Emission Line Spectra Atoms of a gas emit e-m radiation if they become excited. This means the electrons jump to a higher energy level and then fall back, losing potential energy and emitting it as a photon of e-m radiation. This will have a frequency according to ΔE = hf • Experiment: Observing emission spectra • Place a slit in front of a hydrogen lamp. • View the light through a diffraction grating or by refracting it through a prism.
Results: Conclusion Explain why... only certain colours are seen for any particular lamp. coloured fringes are produced This is the image seen when light from one lamp is diffracted through a grating:
Xenon Images from this website
Hydrogen... Helium... Neon...
Absorption spectrum If light with a continuous spectrum of frequencies (a filament light bulb approximately emits this) is shone into a gas its photons will interact with electrons in the gas atoms, boosting them to a higher energy level. Thus the gas will absorb only certain frequencies of the light. These frequencies will be missing from the light that passes through.
Absorption spectrum for Hydrogen. Q. Why des the intensity not fall to zero for the absorption lines? Energy is re-emitted as photons in all directions
Fraunhoffer Lines This effect is visible in the Fraunhoffer lines seen in spectra of light from the Sun. The Sun emits a virtually continuous spectrum. The absorption lines are due to gases in the Sun’s atmosphere absorbing some frequencies of photon. Hence astronomers can deduce what gases are in a star’s atmosphere as well as their proportions.
The ‘Electron in a Box’ Model of an Atom We have seen how the Bohr model of an atom suggests that the atom has discreet energy levels. Thus the energy of the electrons and of the atom is not continuous. Next we will look at how this idea is compatible with the de Broglie hypothesis. According to de Broglie, the electron must have wave properties. So how does this wave fit into an atom...?
We can create a quantum model of an electron trapped in an atom by considering the electron as a standing wave travelling back and forth across a box of side L: Clearly, if there are nodes at either end, the electron can only have certain fixed wavelengths and frequencies. i.e. λ = 2L (fundamental) λ = L (2nd harmonic) λ = 2/3 L (3rd harmonic) So in general λ = 2L n Java applet
According to de Broglie... The KE of the electron is given by KE = ½ mv2 Substituting the equations for v and λ gives… The energy of the electron ‘wave’ is clearly quantised (it has discreet values depending upon n), thus fitting scientific observations e.g. work function in the photoelectric effect. λ = h = h v = h p mv mλ n = integer h, m and L are all constants. KE = n2 h2 8mL2
Limitations of the Bohr Model of the Atom The Bohr model of the atom worked well with basic ideas of quantum theory (as we have seen). However it has limitations. E.g. It only works well with the Hydrogen atom It does not predict intensities of different spectral lines.
Schrödinger's Model of the Atom • Schrödinger developed a new model that accounted for all these limitations. He suggested that... • electrons exist in the atom with a position determined by the wavefunction (ψ – psi), a function of position and time. • the position of the electron at any time is undefined • the probability of the finding the electron at any particular position in the atom is determined by the square of the amplitude of the wavefunctioni.e. ψ2 • Thus for a given energy there are some places where the electron is more likely to exist. This can be represented by ‘probability clouds’.
Additional note: This illustrates an important feature of quantum mechanics. Its outcomes are probabilities and not certainties; it is a probabilistic model. Classical mechanics (e.g. Newtons laws) are deterministic: the future is determined by the past and is therefore predictable with some certainty!