A chess puzzle

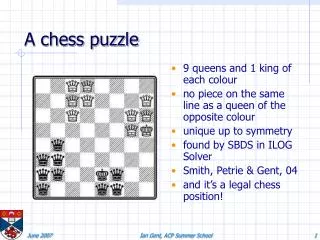
1. A chess puzzle • 9 queens and 1 king of each colour • no piece on the same line as a queen of the opposite colour • unique up to symmetry • found by SBDS in ILOG Solver • Smith, Petrie & Gent, 04 • and it’s a legal chess position! Ian Gent, ACP Summer School

2. Symmetry in Constraint Programming Ian Gent St Andrews

3. Symmetry in Constraint Programming Ian Gent St Andrews Special thanks to … Jean-François Puget ILOG, France

4. Special thanks toKaren Petrie OxfordBarbara Smith LeedsIan Miguel St AndrewsAlan Frisch YorkColva Roney-Dougal St AndrewsSteve Linton St AndrewsSarah Gent Castlehill School “A project of this scope and importance could not be achieved without the aid and assistance of many people… …. or rather it could but it would be dumb to do it that way when there are so many people around willing to give their aid.” - Peter Schickele

5. Shameless self promotion • A most excellent survey has recently been written…. • “Symmetry in Constraint Programming” • Ian Gent, Karen Petrie, Jean-François Puget • In “Handbook of Constraint Programming” • Ed. Rossi, van Beek, & Walsh • Elsevier, 2006 • I can give you a copy if you are interested • Error in paper: (noticed by Pedro Meseguer) • Example 10.2 p 332 • Cyclic forms of r90 and r270 are wrong. • r90 should be (1 7 9 3) (2 4 8 6) • r270 should be (1 3 9 7) (2 6 8 4) Ian Gent, ACP Summer School

6. Summer Schools are Great… • They can lead to untold happiness • Joy • Delight • You think I’m kidding? • How did a British person meet an American in Germany in 1991? Ian Gent, ACP Summer School

7. Ian Gent, ACP Summer School

8. How to get here:Giving Lectures at Summer School • Do a PhD in something else. • Go to a summer school in that. • Follow the stupidest dating strategy in the world (for a man). • Change area and do something completely different. • Get into constraints. • Work on something completely different • Write a paper on symmetry. • Think that there is not much future in the area. • Work with people smarter than you. • Write lots of papers with them. Ian Gent, ACP Summer School

9. Free advice • Dotted throughout lectures will be some free advice on being an academic • Well it’s not really free • Since you paid to be here • And you might have seen it before • In doctoral programme of CP 06 • And it may be rubbish • Check out my dating advice • BUT without any question at all • It is advice. Ian Gent, ACP Summer School

10. Best free advice I can give • Work with people smarter than you. • Be the stupidest person you work with! • Most people are scared of working with smarter people. • They feel good if they are smarter than their colleagues. • Think of it this way: • Most computer scientists collaborate. • The smarter the group the better the output tends to be. • You can’t make yourself more intelligent quickly. • Find the smartest people you can who don’t think it’s a waste of their time working with you. • Or think of it this way: • Will your paper be better if your co-authors are • smarter than you or • stupider than you? • P.s. I applied this to my choice of wife as well :-) Ian Gent, ACP Summer School

11. Always be the stupidest person you work with! • So if you constantly feel you are the stupidest one in the room • Try to feel good about it! • I should know …. • Since I’ve worked with … • Joe Culberson, Jeremy Frank, Enrico Giunchiglia, Warwick Harvey, Holger Hoos, Chris Jefferson, Tom Kelsey, Steve Linton, Inês Lynce, Ian Miguel, Massimo Narizzano, Pete Nightingale, Karen Petrie, Patrick Prosser, Andrea Rendl, Colva Roney-Dougal, Andrew Rowley, Kostas Stergiou, Paul Shaw, Barbara Smith, Toby Walsh, … • … and Judith Underwood. Ian Gent, ACP Summer School

12. Section 10.1, p331 Group Theory • What is a group? • Standard mathematical answer is: • Group = pair of set and operation <G,*> with • For all g,h in G, g*h in G • There is 1 in G such that for all g in G, 1*g = g*1 = g • For all g in G, there is g-1 such that g*g-1 = 1 • For all g,h,j in G, (g*h)*j = g*(h*j) • What has this got to do with symmetry? • Ordinary answer: • A group is an organisation of people. • Unfortunately not the answer we need! • What’s the link between groups and symmetries? Ian Gent, ACP Summer School

13. Group Theory • Let’s start again. • Mathematics deals with abstractions • E.g. • Abstraction of repetition  Integers • Abstraction of continuous quantities  Real numbers • Similarly • Abstraction of symmetry  Group Theory Ian Gent, ACP Summer School

14. Group Theory • I want to explain tiny bits of group theory • Explaining relevance to Constraints • Eventually we’ll see why group axioms hold • Introduce a few key concepts that come up • I am going to focus on • The action of group elements • Not usually focus of simple introductions • But what constraint programmers need to think about • Group elements as permutations Ian Gent, ACP Summer School

15. 8 symmetries of the square Ian Gent, ACP Summer School

16. Rotation though 90 degrees: r90 • Two ways to think about this • 1 moves to 3, 2 moves to 6 … • 1 is replaced by 7, 7 is replaced by 9 … • In the paper we used the second version • sometimes getting it wrong, sorry. Ian Gent, ACP Summer School

17. This defines an action on points • This is a permutation • Each point is mapped to exactly once • Above is written in Cauchy form Ian Gent, ACP Summer School

18. This defines an action on points • Presentations more normally written in cycle form • (1 7 9 3) (2 4 8 6) (5) • (1 7 9 3) (2 4 8 6) Ian Gent, ACP Summer School

19. Where have we got to? • A symmetry is a mapping of an object • E.g. r90 is a function on a square • Leaves some features unchanged • It is still a 3x3 square • We label the object with points • The Symmetry possibly changes those points • E.g. 1 is replaced by 7 • A permutation summarises the changes made • Where each point is moved to • The permutation is a permutation of the points • We say that the symmetry acts on the points • E.g. 1r90= 7 • Action can be extended to sets of points • E.g. {1,3,8} r90 = {1 r90, 2 r90, 3 r90} = {7,1,6} = {1,6,7} Ian Gent, ACP Summer School

20. Composition of Permutations • Two symmetries acting in a row compose • Permutations compose in the same way • E.g. • r90 = (1 7 9 3) (2 4 8 6) • x = (1 3)(4 6)(7 9) (reflection about centre col) • r90 * x = (1 9)(2 6)(4 8) • NOTE: in r90 * x, r90 is done first • 1 r90 * x= (1 r90 ) x= 7 x= 9 Ian Gent, ACP Summer School

21. Identity and inverse • Permutations make identity and inverse easy • Identity: • () in cycle form • In Cauchy form 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 • Inverse • Just reverse each (..) in cycle form r90 = (1 7 9 3) (2 4 8 6) r90 -1 = (3 9 7 1)(6 8 4 2) = (1 3 9 7)(2 6 8 4) = r270 Ian Gent, ACP Summer School

22. Associativity • (f * g) * h = f * (g * h) • Basically function application always respects this • Doing (f and then g) and then h • Is the same as doing f and then (g and then h) • Because of the way we thought about composition, there is nothing to say Ian Gent, ACP Summer School

23. Group Axioms again • Group = pair of set and operation <G,*> with • For all g,h in G, g*h in G • There is 1 in G such that for all g in G, 1*g = g*1 = g • For all g in G, there is g-1 such that g*g-1 = 1 • For all g,h,j in G, (g*h)*j = g*(h*j) • G = set of permutations • E.g. {1, r90, r180, r270, x, y, d1, d2} • See? Elements of the group are themselves functions. They act on the points in our square • * = composition of permutations • Composition of two permutations is another permutation • () is the identity permutation • We’ve seen how to get the inverse • Associativity is fundamental Ian Gent, ACP Summer School

24. Generators • Number of elements is order of the group • Closure and inverse lets us generatea group from a small number of elements. • E.g. chessboard from {r90,x} • The maximum size of a (minimal) generating set for a group of order n is log2 n • Typically groups of arbitrary size can be generated by 2 elements! • Use of generators fundamental in computational algebra • Can save exponential space • Can be vital for time as well • Don’t want to step through exponential elements. Ian Gent, ACP Summer School

25. Moving right along • Going to mention a few things briefly • Subgroup • <H,*> a subgroup of <G,*> if H subset of G and H closed under * • Coset • If H is a subgroup of G and g any element of G • Then a left coset g * H = { g * h | h in H} • Two cosets g * H, f * H are equal or disjoint • All cosets are of size | H | • Hence Lagrange’s theorem • order of subgroup divides order of group • A set of coset representatives is a set R subset of G • Such that, for all g in G, g*H = r*H for some r in R Ian Gent, ACP Summer School

26. Orbit & Stabiliser • The orbit of a point p in group G is • pG = {pg | g in G} • I.e. everywhere a point can be moved to by elements of G • The stabiliserof a point p in G is • Gp = {g | g in G and pg=p} • I.e. set of points that fixes p • Stabiliser is always a subgroup of G. Ian Gent, ACP Summer School

27. Section 10.1.2, p337 Schreier Sims • Key algorithm in computational algebra • Akin to Arc Consistency in Constraint Satisfaction • You may need to implement it one day • Computers a stabiliser chainand a set of coset representatives at each level • Say we have listed points in order 1, 2, 3 … n • G0 = G • G1 = (G0)1 • G2 = (G1)2 • … • Gi = (Gi-1)I • … • Gn = {1} (since only identity fixes every point) • Schreier Sims computes the stabiliser chain efficiently AND gives a data structure storing this and the set of coset representatives at each level. Ian Gent, ACP Summer School

28. Tip Never read reviews the day your paper is accepted or rejected

29. Never read reviews the day your paper is accepted or rejected • About 15 years ago Alan Bundy said … • … getting reviews always ruined his day • Even for accepted papers! • For accepted papers? • One reviewer is negative • One is lukewarm • One reviewer misses the point completely • They suggest changing the title you love • Get over the news first • Enjoy it, celebrate, look forward to a trip, consider how clever you must be to publish in International Symmetry Conference • Get over it, get on with your life, consider how lucky you are not to have to go to the International Symmetry Conference, what with stupid flights and AAAI next year is a much better conference • Then read the reviews the next day Ian Gent, ACP Summer School

30. 8 symmetries of the square Ian Gent, ACP Summer School

31. A chess puzzle • 9 queens and 1 king of each colour • no piece on the same line as a queen of the opposite colour • unique up to symmetry • found by SBDS in ILOG Solver • Smith, Petrie & Gent, 04 • and it’s a legal chess position! Ian Gent, ACP Summer School

32. Symmetry Breaking in Constraint Programming • Many constraint problems have symmetry • n-queens, colouring, golfers’ problem, … • Breaking symmetry reduces search • avoids exploring equivalent states • not sure if “breaking symmetry” is right term, but we’re stuck with it • in fact preferring (using some method) a subset (preferably singleton) of each equivalence classe • Note that main goal is pragmatic • make constraint programming more effective Ian Gent, ACP Summer School

33. Symmetries • Isomorphisms • 1-1 Mappings (bijections) that preserve problem structure. • Variables can be permuted • Values can be permuted • Both • Map solutions to solutions • Potentially large number of isomorph variants • Map trees search to tree search • The same failure will be repeated many times Ian Gent, ACP Summer School

34. Section 10.2, p337 Symmetry Definitions • Not really sorted out until 2005! • Cohen, Jeavons, Jefferson, Petrie, Smith • What was going on until then? • Can think of symmetries semantically or syntactically • Solution Symmetry • A permutation of the variable-value pairs which leaves the set of solutions unchanged • Problem Symmetry • A permutation of the variable-value pairs which leaves the set of constraints unchanged • All problem symmetries are solution symmetries, but not vice versa • Cohen et al go into more detail with interesting results Ian Gent, ACP Summer School

35. Variable and Value symmetries • Variable Symmetry • A symmetry which only changes variables • E.g. (x=1)g = (y=1) leaves the value 1 unchanged • Value Symmetries • A symmetry which only changes values • E.g. (x=1)g = (x=7) leaves the variable x unchanged • Various pieces of research in constraints focus on one or the other. • Sometimes for fundamental reasons • Sometimes for convenience Ian Gent, ACP Summer School

36. Section 10.1.1 p336 Constraints and Group Theory • Typically, points = set of variable-value pairs • E.g. if n variables with m values, nm points. • Sometimes only n if dealing with variable symms. • Or only m if dealing with value symms • Permutations act on these points (v-v pairs) • Set of permutations defines the group Ian Gent, ACP Summer School

37. Section 10.8, p365 Getting Symmetry in the System • How does a constraint program know about symmetry? • Most work assumed symmetries given by the programmer • Which isn’t realistic in practice • Attempts to get simple language to express symmetries • E.g. in ECLiPSe symmetry libraries • Significant efforts on detecting symmetries • Almost inevitably problem symmetries, not solution ones • Use graph of some representation of the problem • Use graph automorphism software on the result • E.g. Aloul et al in SAT, Puget in CP Ian Gent, ACP Summer School

38. Symmetry Breaking in Constraint Programming • Three main approaches to symmetry breaking • reformulate the problem • adapt search algorithm to break symmetry • add constraints before search Ian Gent, ACP Summer School

39. Symmetry Breaking in Constraint Programming • Three main approaches to symmetry breaking • reformulate the problem • adapt search algorithm to break symmetry • add constraints before search Ian Gent, ACP Summer School

40. Section 10.3, p340 Symmetry Breaking by Reformulation • Reformulation can be the most effective means to break symmetry • As yet, there is very little general to say about it • general methods and/or theorems would be welcome • This is a common feature in AI • we know problem representation is vital • we don’t know how to exploit it except by magic Ian Gent, ACP Summer School

41. An example • Crew assignment • One variable per crew staff : x[j] • One value per crew : a[i] • A size per crew : c[i] x in a; distribute(x,card,a); forall (i) card[i] <= c[i]; • Add x[1] <= x[2] <= … <= x[n] breaks variable permutations card[1] >= card[2] >= … >= card[n] breaks value permutations Ian Gent, ACP Summer School

42. Problem reformulation • Use set variables if possible • For the crew example, use A set variable s[i] per crew A value per staff. • This breaks permutations of people • Add card(s[1]) >= card(s[2]) >= … >= card(s[n]) • This breaks permutations of crews Ian Gent, ACP Summer School

43. Reformulation example • All Interval Series Problem • Write down the numbers 0…n-1 • so that each difference 1...n-1 occurs between consecutive terms • e.g. 0 8 1 7 2 6 3 5 4 • diff 8 7 6 5 4 3 2 1 • now count number of solutions • Symmetries: reverse sequence & complementation • This problem is not important but there is a dramatic reformulation Ian Gent, ACP Summer School

44. Reformulation example • Reformulated All Interval Series Problem • write down the numbers 0…n-1 in a cycle • so that each difference 1...n-1 occurs between consecutive terms and one difference occurs exactly twice • e.g. 0 8 1 7 2 6 3 5 4 • diff 8 7 6 5 4 3 2 1 4 • now count number of solutions • Symmetries: reverse sequence & complementation • & rotation of sequence by j steps • Each solution yields two solutions to the original • e.g. 6 3 5 4 0 8 1 7 • We can break all symmetry very easily • set first 3 terms to be 0 n-1 1 • Improved the state of the art by a factor of 50 in run time Ian Gent, ACP Summer School

45. Tip Do read negative reviews

46. Do read negative reviews • There is always the amazing possibility that the person who wrote the review… • … is notan idiot • Even if they are an idiot… • … there may be other idiots out there • … who will review your future papers! • Try to make the changes they want • Correct typos, redo experiments, clarify explanations… • Look out for patterns in reviews • You might be making the same mistake again and again • After all this you will think your papers are better Ian Gent, ACP Summer School

47. Symmetry Breaking in Constraint Programming • Three main approaches to symmetry breaking • reformulate the problem • add constraints before search • adapt search algorithm to break symmetry Ian Gent, ACP Summer School

48. Section 10.4, p343 Symmetry Breaking Constraints • Probably the grandmother of symmetry breaking constraints • Added ad hoc since the beginning of time • e.g. • X <= Y <= Z … if S_n acts on variables • the first queen is to the left of the second queen • Difficult to be sure you have eliminated all symmetry • Requires considerable insight from programmer • Some symmetries require large constraints • But easy for constraint programming systems to cope with Ian Gent, ACP Summer School

49. Section 10.4.1, p343 Lex-Leader • Crawford, Ginsberg, Luks & Roy, 1996 • biggest single advance in symmetry breaking in SAT & Constraints? • Idea essentially simple • Define a canonical solution and add constraints to choose it • Note: technically only applies to variable symmetries. Recently extended by Puget and Walsh (separately, CP06). Ian Gent, ACP Summer School

50. Canonical solutions • Assume an ordering on variables • Define an ordering on solutions • How to compare two solutions a and b? • Use a lexicographic ordering: • Write the values in the order given by the variable ordering • Compare the two numbers obtained this way • A canonical solution s is smaller than any of its symmetrical variant • S ≤Lex g(s), for all symmetries g. Ian Gent, ACP Summer School